塑性勢

塑性勢(plastic potential)是表征塑性應變增量同載入曲面關係的“勢函式”，也是對應力分量內的偏導數求出，即式中dλ是一非負的瞬時比例係數。1928年Mises參照彈性應變增量用彈性勢函式對應力的偏導數表達式，從而提出了塑性勢的概念。

基本介紹

• 中文名：塑性勢
• 外文名：plastic potential
• 類型：塑性應變增量同載入曲面的勢函式
• 提出者：Mises
• 提出時間：1928年
• 學科：力學

塑性勢理論

在德魯克公設（Drucker postulate）提出來之前，人們並不了解塑性應變增量與載入面有什麼關係，在1928年Mises類比了彈性應變可用彈性勢對應力求偏導的表達式，提出了塑性勢的概念，其數學形式是

式中 g 是塑性勢函式，它是應力 σ_ij和內變數 ζ_β的標量函式，在屈服和硬化為各向同性的情況下，它可以表示為應力不變數和內變數的函式。式中左側分量表示的單位體積的彈性應變能。1957年布蘭德 (D.R.Bland)證明，塑性勢和米澤斯屈服函式是同一函式，因此也稱為米澤斯屈服函式。據此，可導出普朗特-羅伊斯函式，通過用f(σ_ij)作為塑性勢g，可使米澤斯屈服條件與增量理論以更加一般的形式聯繫起來。 屈服函式f(σ_ij)作為塑性勢，可得應力點屈服後產生的塑性應變增量構成的合成向量同f(σ_ij) 曲面上該應力點的外法線方向一致。

對於服從德魯克公設的穩定材料而言，應取屈服函式 f 作為塑性勢函式 g，即取 g=f，這樣就將屈服函式與塑性本構關係聯繫起來考慮。一般地，將 g=f 的塑性本構關係稱之為與屈服函式相關聯的流動法則，若 g≠f 則稱之為非關聯的流動法則。在非關聯的流動法則下，塑性應變增量與屈服面不正交。非穩定材料如岩土材料的塑性本構關係一般認為服從非關聯的流動法則。

塑性勢與流動理論

在塑性位勢理論中，塑性應變率分量（或無限小塑性應變率）的比例關係定義為

式中，g 和 h 均為應力偏量不變數的函式；f 為屈服函式（如果 df=0 ，表示中性載入，則 df<0 表示卸載）；函式 g 稱為塑性位勢。儘管上式以率的形式給出，但它並不表示真正的時間概念。

假設 g=f ，則上式變為

式中，dλ 為一非負比例常數，等於 hdf 。上式表示了與屈服函式f(σ_ij) 相關的流動規則。

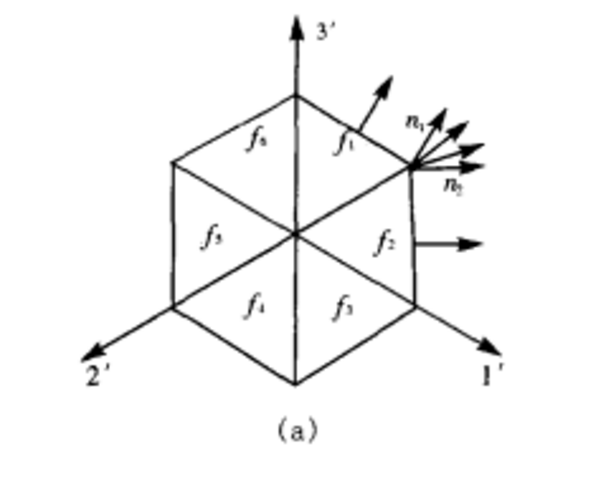
將應力空間 σ_ij與塑性形變空間的坐標重合，並引入一個因子G，G 的大小使得塑性應變率矢量的度量七點位於屈服面上，由於，即塑性體積不變條件，則塑性應變率矢量必位於π平面內。同時，因為表示屈服表面f(σ_ij)=C 的外法線方向餘弦，則該塑性應變率矢量必然垂直於點（σ'_1，σ'₂，σ'₃）處的屈服軌跡。如右圖所示，PO代表塑性應變率（）矢量，它垂直於P點的米席斯屈服圓。塑性位勢的概念及其相關的流動法則也可用於屈雷斯加屈服條件。應當注意，若對於給定的塑性應變率存在唯一對應的應力時，則屈服軌跡必須處處外凸。