基本介紹
- 中文名:基本最優解
- 外文名:basic optimal solution
- 所屬學科:數學
- 所屬問題:線性規劃
- 簡介:使目標函式達到最優值的基可行解
基本介紹






求解方法















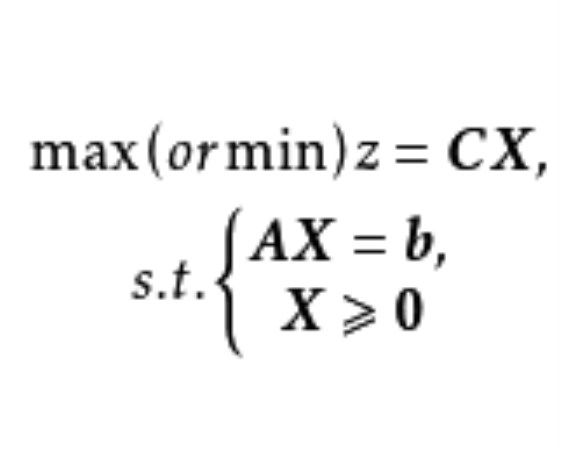





















基本最優解(basic optimal solution)是線性規劃的重要概念,指線性規劃問題中使目標函式達到最優值的基可行解。基本介紹考慮標準型LP問題設A是階矩陣,,且A的秩為m。可行解:滿足上述約束條件(2)、(3...
數學規劃的基本概念之一。指在數學規劃問題中,使目標函式取最小值(對極大化問題取最大值)的可行解。使目標函式取最小值的可行解稱為極小解,使其取最大值的可行解稱為極大解。極小解或極大解均稱為最優解。相應地,目標函式的...
若存在有界最優解,則至少有一個基本可行解為最優解。基本介紹 線性規劃中的約束條件除變數非負性限制外都採用等式約束,線性規劃問題的一般形式為 式中 AX = B 稱為約束方程,A 為係數矩陣,B 為常數向量,稱為變數非負約束。
主要研究內容有:線性組合最最佳化問題;網路上的最最佳化問題;獨立系統和擬陣,擬陣是組合最佳化中一個基本而重要的概念,許多組合問題都可化為擬陣問題。貪心算法是求擬陣的最優獨立集的簡單算法;交錯鏈算法是求解最優交問題的基本算法。對...
《戰略思維:快速尋找複雜問題的最優解》是中信出版集團2022年11月出版的圖書,作者是[英] 弗雷德·佩拉德(Fred Pelard),由王建志翻譯。內容簡介 擁有戰略思維是一項重要技能。它既能幫你解決眼前的基本問題,又能使你著眼於長遠、...
求解的思路是:先將約束條件加以圖解,求得滿足約束條件的解的集合(即可行域),然後結合目標函式的要求從可行域中找出最優解。基本概念 可行解 把滿足約束條件的一組決策變數值 稱為該線性規劃問題的可行解。可行解集/可行解域 滿...
2.判定最優解。基可行解為線性目標規劃的滿意解,而基可行解為線性規劃的基本最優解,故用單純形法(參見“單純形法”)求解其對應的線性規劃問題得到的基本可行解也是線性目標規劃的滿意解.3.換基疊代.若檢驗數不符合基本原理2(...
基於此,單純形法的基本思路是:先找出可行域的一個頂點,據一定規則判斷其是否最優;若否,則轉換到與之相鄰的另一頂點,並使目標函式值更優;如此下去,直到找到某最優解為止。基本單純形法 單純形法的基本想法是從線性規劃可行集...
基本原理 所謂滿足對偶可行性,即指其檢驗數滿足最優性條件。只要保持檢驗數滿足最優性條件前提下,一旦基解成為可行解時,對偶問題和原問題均可行,由強對偶性證明,二者均有最優解。設原始問題的標準形式為max{cx|Ax=b,x≥0},...
所謂最優性檢驗就是判斷已求得的基本可行解是否是最優解。對於求最大目標函式的問題中,對於某個基本可行解,如果所有檢驗數 ,則這個基本可行解是最優解。對於求目標函式最小值的情況,只需把 改為 。確定方法 在單純形法的...
只要將有限個點逐一比較目標值的大小,該問題最優解就一定可以得到。但是枚舉是以時間為代價的,有的枚舉時間還可以接受,有的則不能接受。設問題的規模為n,如果存在一個多項式p(n),使得算法最多執行p(n)個基本步驟便可得到解答,...
(1)用西北角規則或最小元素法確定初始基本可行解;(2)用位勢法求檢驗數;(3)用閉迴路調整法調整基本可行解。基本概念 基格和非基格 定義1:將變數 在調運表中所對應的空格記作(i,j),稱為格點(i,j)或格(i,j)。
如果線性規劃問題中的a、b或c等參數值與這個代表M的數比較接近,或遠遠小於這個數字,由計算機計算時有可能使計算結果發生錯誤,從而使求解的最終結果與原問題真正的最優解不一致。為了克服這個困難,可以對添加人工變數後的線性規劃問題分...
百分之一百法則是指對於所有變化的約束條件中的常數項,當其所有允許增加百分比和允許減少百分比之和不超過百分之一百時,其對偶價格不變。基本概念 容許增加(或減少)量是指目標函式的某個係數單獨發生變化時最優解保持不變時在上(或...
圖解法一般是指求解僅含兩個變數的線性規劃問題的一種方法。只含兩個變數的線性規劃問題,由約束條件確定的可行域可以在二維平面上表示出來,按照一定規則,在可行域上移動目標函式的等值線,從而得到線性規劃問題的最優解。這裡的可行域...
3、改進當前的基本可行解(確定換入、換出變數),用閉合迴路法調整;(因為目標函式要求最小化)表格中有調運量的地方為基變數,空格處為非基變數。基變數的檢驗數 ,非基變數的檢驗數 。表示運費減少,表示運費增加。4、重複②,...
梯度投影法(gradient projection method)利用梯度的投影技巧求約束非線性規劃問題最優解的一種方法。求帶線性約束的非線性規劃問題更為有效。它是從一個基本可行解開始,由約束條件確定出凸約束集邊界上梯度的投影,以便求出下次的搜尋方向...
單純性算法,計算機科學術語。單純形法是一種疊代算法,其基本原理及主要步驟是:首先設法找到一個(初始)基可行解,然後再根據最優性理論判斷這個基可行解是否最優解。若是最優解,則輸出結果,計算停止;若不是最優解,則設法由當前...
貪心算法不是對所有問題都能得到整體最優解,關鍵是貪心策略的選擇。算法思路 貪心算法的基本思路是從問題的某一個初始解出發一步一步地進行,根據某個最佳化測度,每一 步都要確保能獲得局部最優解。每一步只考慮一 個數據,其選取...
貪心算法不是對所有問題都能得到整體最優解,關鍵是貪心策略的選擇,選擇的貪心策略必須具備無後效性,即某個狀態以前的過程不會影響以後的狀態,只與當前狀態有關。基本要素 貪心選擇 貪心選擇是指所求問題的整體最優解可以通過一系列...
