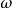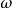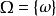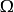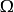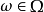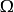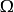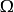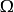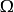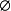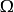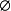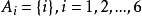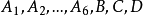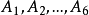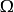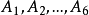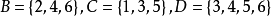基本事件空間亦稱樣本空間，機率論的基本概念之一，是機率論研究的出發點。隨機試驗的每一個單一的結果稱為一個基本事件，全體基本事件的集合稱為基本事件空間，一般以ω表示基本事件，以Ω表示基本事件空間。基本事件空間又常稱為樣本空間，此時，基本事件稱為樣本點。只含有有限個基本事件(樣本點)的基本事件空間稱為有限基本事件空間(有限樣本空間)；含有可數個基本事件(樣本點)的基本事件空間稱為離散基本事件空間(離散樣本空間)。如果拋開基本事件的具體定義，則可以把Ω看成一個抽象點集，每一個基本事件ω就是Ω中的一個點，基本事件空間可以根據隨機試驗的內容(試驗條件與觀察的目的)來決定。例如，從標有1，2，3，4，5，6號碼的六張卡片(其中4張紅色，2張白色)中任取一張，觀察所抽得的號碼，則基本事件空間為Ω1={1，2，3，4，5，6}；若觀察所抽得的卡片顏色，基本事件空間為Ω2={紅色，白色}。
基本介紹
- 中文名：基本事件空間
- 外文名：space of elementary event
- 所屬領域：是機率論的基本概念之一
- 別稱：樣本空間
- 定義：全體基本事件的集合
基本介紹,空間概念,例題解析,隨機事件,
基本介紹
在實際中，我們常常通過隨機試驗(即在某個條件C下)來研究隨機事件，這裡所指的試驗是一個廣義的術語，它包括各種各樣的科學實驗，也包括對某一事物的某一特徵的觀察等。一般地，設E為一試驗，如果不能事先準確地預見它的結果，而且在相同條件下可以重複進行，就稱為隨機試驗。
空間概念
對於一個隨機試驗E來說，首先要知道這個試驗可能出現的結果，若以
表示它的一個可能的結果，就稱 為E的一個基本事件(或樣本點)，全體基本事件的集
稱為基本事件空間(或樣本空間)。在具體問題中，十分重要的是要認清基本事件空間
是由什麼構成的，它是描述隨機現象的第一步。
需要說明的是，基本事件空間 是由那些“不能或不必再分”的隨機事件叫所組成，使得在每次試驗或觀察下有一且僅有一
發生，當然，對於一個實際問題或隨機現象，如何用一個恰當的基本事件空間來描述它也值得研究．但在機率論的研究中，一般都認為基本事件空間是給定的，這是必要的抽象，這種抽象使我們能更好地把握隨機現象的本質，而且得到的結果可以更廣泛地套用。事實上，一個基本事件空間可以概括各種實際內容大不相同的問題，例如，只包含兩個基本事件的基本事件空間既能作為產品檢驗中出現“合格品”與“不合格品”，也能作為擲硬幣出現“正面”及“反面”的模型，又能用於氣象中“下雨”與“不下雨”，以及排隊現象中“有人排隊”與“無人排隊”等．儘管問題的實際內容如此不同，但有時卻能歸結為相同的模型。
例題解析
例1某袋中裝有4隻白球和2隻黑球，考慮依次從中任意摸出兩球時可能出現的情況．若對球進行編號，4隻白球分別編為1，2，3，4號，2隻黑球編為5，6號．若用數對(i，j)來表示第一次摸得j號球，第二次摸得i號球，則可能出現的結果是：
(1，2)， (1，3)， (1，4)． (1，5)， (1，6)，
(2，1)， (2，3)， (2，4)， (2，5)， (2，6)，
(3，1)， (3，2)， (3，4)， (3，5)， (3，6)，
(4，1)， (4，2)， (4，3)， (4，5)， (4，6)，
(5，1)， (5，2)， (5，3)， (5，4)， (5，6)，
(6，1)， (6，2)， (6，3)， (6，4)， (6，5)．
把這30種可能結果作為樣本點，則構成了樣本空間。在該問題中，我們還對下面這些隨機現象感興趣：
A：第一次摸出黑球；
B：第二次摸出黑球；
C：第一次及第二次都摸出黑球．
這些事件與前面那些基本事件的不同之處在於這些事件是可以分解的，例如，A要出現必須且只須下列可能結果之一出現：
(5，1)，(5，2)， (5，3)， (5，4)， (5，6)，
(6，1)，(6，2)， (6，3)， (6，4)， (6，5)．
隨機事件
有了基本事件空間的概念，就可以定義一般的隨機事件，在例1中前面30個事件是由單個基本事件構成的，而後面這3個事件A、B、C都是由若干個基本事件所構成，總之，它們均為基本事件的某個集合，即為基本事件 空間的一個子集。
我們就將樣本空間的一個子集稱為一個隨機事件，簡稱事件，通常用大寫字母表示，因此，隨機事件就是試驗的若干個結果組成的集合，如果一個隨機事件只含一個試驗結果，它即為基本事件，可以看出，某事件的發生(出現)是若且唯若它所包含的某一基本事件發生。
在這裡，事件這一名詞不是通常意義下的概念，例如某礦難事件、1941年日本偷襲珍珠港事件之類的，它們往往指一種已發生的情況。在機率論中則不然，事件不是指已發生的情況，而是指某類現象，它可能發生，也可能不發生，具有隨機性，它的發生與否要到實驗或觀察之後才能知曉．另外，由於樣本空間 包含了所有的樣本點，且是 自身的一個子集，在每次試驗中它總是發生的，所以稱 為必然事件，它對應了必然現象，空集
不包含任何樣本點，它也是樣本空間 的一個子集，且每次試驗中總不會發生，所以稱 為不可能事件，它對應了不可能現象，這樣處理是為了今後研究的方便。
例2擲一個均勻的骰子，用
分別表示所擲的點數，B表示“偶點數”，C表示“奇點數”，D表示“3點或3點以上”，試寫出樣本空間，指出
事件中哪些是基本事件，並表示事件B，C，D。
解: 拋擲後有6種不同的結果，即
，樣本空間={1，2，3，4，5，6)；是基本事件，而事件
。
