埃文斯定理

埃文斯定理是描述零容集與位勢的關係的論斷，亦稱為埃文斯-塞爾貝格定理。

基本介紹

• 中文名：埃文斯定理
• 外文名：Evans theorem
• 適用範圍：數理科學

簡介

埃文斯定理是描述零容集與位勢的關係的論斷，其推廣形式分如下三種情形敘述：

1.若E是Rⁿ(n≥3)的G_δ集且牛頓容量為零，則存在μ≥0，使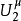在E上且僅在E上取+∞值並有μ(Rⁿ\E)=0（從而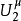在Rⁿ\E內調和）；

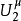
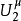
2.若E是R²的零容緊集，則有相應的對數位勢滿足1中條件；

3.若在Rⁿ(n≥2)考慮α容量為零的G_δ集E，仍存在僅在E上取+∞值的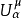，但μ(Rⁿ\E)=0未必成立，當E為緊集時則成立。上述位勢常稱為埃文斯位勢。

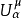
背景

由於埃文斯(Evans,U.C.)與塞爾貝格(Selberg,A.)同時於1935年獨立地就E是緊集的情形給出結論1，因此，上述定理亦稱為埃文斯-塞爾貝格定理。

位勢

一般位勢是經典位勢的一種直接推廣形式，常為一個二元數值函式（核）關於某個測度的積分。

設(Ω,𝓕)是一個可測空間，K(x,y)是從Ω×Ω到[-∞,+∞]的可測函式，μ是𝓕上的實測度。若對每個x∈Ω，下式中的積分有意義，則由Ω到[-∞,+∞]的函式

稱為μ以K為核的一般位勢，簡稱位勢。