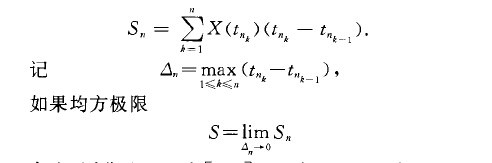
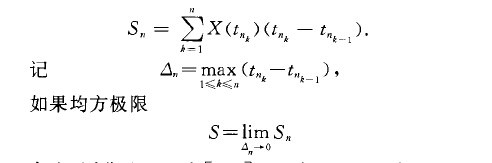
均方積分(integral in mean square)隨機分析的基本概念之一設{XCt),tE巨，司}是一個二階矩過程，對區間[}a ,司的任一划分:a=tnoCtnlCwCt i=b，定義黎曼和
存在，則稱此過程在山 ,川上均方可積，而稱S為此過程在[a ,川上的均方積分，並記為
其中m(t),R(s,t)及I'(s,t)分別是{X(t),tE[u,b]}的均值函式、相關函式及協方差函式.
均方積分
相關詞條
- 均方積分
均方積分(integral in mean square)隨機分析的基本概念之一設{XCt),tE巨,司}是一個二階矩過程,對區間[}a ,司的任一划分:a=tnoCtnlCwCt i=b,定義黎曼和...
- 均方導數
均方導數是高等數學中的導數是隨機過程在均方意義下的推廣,其許多性質也是相同。...... 隨機過程在均方意義下的極限、連續、導數和積分的定義在形式上與高等數學中...
- 伊藤積分
若無限分細時,此和式有唯一的均方極限,則稱該極限為 在 上的伊藤積分,記作定理:若 在 上連續,對任意 ,都有 與 獨立,則存在。...
- 隨機積分
的均方極限存在,記作隨機積分,它稱為φ在區間【α,b】上對W 的伊藤積分。值得注意的是,在達布和的構造中,被積過程在【tk-1,tk】上的取值點不是隨意一點,...
- 機率論及數理統計(下冊)
二、隨機過程的均方連續 三、隨機過程的均方積分 四、隨機過程的均方導數 五、隨機微分方程 11.6 平穩隨機過程 一、定義及例 二、相關函式 三、弱平穩隨機過程...
- 隨機過程引論
4.2.1 均方連續性4.2.2 均方導數4.2.3 均方導數的性質4.3 二階矩過程的均方積分4.3.1 均方積分的定義和準則4.3.2 均方積分的性質...
- 研究生系列教材:隨機過程
全書共分7章,內容包括機率論的補充知識、隨機過程的基本概念、二階矩過程的均方微積分、平穩過程、馬爾可夫過程、更新過程與馬爾可夫更新過程、非平穩隨機過程。...
- 隨機過程(李裕奇,劉赬,王沁編著圖書)
本書內容主要包括隨機過程的基本概念、隨機過程的分布與數字特徵、均方微積分、著名的泊松過程、平穩過程、馬爾可夫過程等隨機過程的基本理論與簡單套用,以及時間序列的...
- 隨機過程(第3版)習題解答
是國防工業出版社出版、李裕奇等編寫的《隨機過程》(第3 版)一書的配套教材,內容包括機率論基礎知識、隨機過程的基本概念、均方微積分、泊松過程、平穩過程、...
- 南開大學公共數學系列教材·經濟套用數學教程
隨機過程初步部分介紹了隨機過程的分布與數字特徵、均方微積分、馬爾可夫鏈和平穩過程等。這些內容都是經濟學(也是管理學)研究與套用中最重要、最基本、最常用的...
- 隨機過程及其套用(第2版)
本書的內容大體可以分為三個部分:Gauss過程和Poisson過程作為最基本最典型的隨機過程,例如以讀者熟悉的“距離”概念為基礎來建立均方意義下的隨機微積分,從確定性...
