圖論算法

圖論算法在計算機科學中扮演著很重要的角色，它提供了對很多問題都有效的一種簡單而系統的建模方式。很多問題都可以轉化為圖論問題，然後用圖論的基本算法加以解決。

基本介紹

• 中文名：圖論算法
• 學科：計算機科學
• 屬性：一種簡單而系統的建模方式
• 地位：很重要的角色

題目

一、求出這個圖的補圖　 （1）輸入無向圖的各邊所關聯的頂點對，確定每個頂點度，以及圖的最大度數和最小度數，求出這個圖的補圖。

（2）輸入有向圖的各邊所關聯的頂點對，確定每個頂點的出度和入度。

二、　編寫一個程式，要求於無向圖和有向圖都能做到：輸入圖的鄰接矩陣和正整數n，求長度為n的鏈和圈。

三、模擬判斷一個程式中是否存在遞歸的函式，若存在，如何消除遞歸。

四、輸入圖的邊，確定這是否為連通圖。

（1）若不是連通圖，則確定連通分圖的個數；

（2）若是連通圖，判斷是否存在割邊和割點，若存在各是什麼？

五、輸入一個多重圖各邊關聯的頂點對。

（1） 判斷它是否存在歐拉圈，若存在，則求出一個歐拉圈；

（2）若不存在，則判斷是否存在一個歐拉鏈，若存在則求之。

六、輸入一個簡單圖的邊列表。

（1）確定是否存在哈密爾頓圈，若存在求該哈密爾頓圈；

（2）若不存在，判斷是否存在哈密爾頓鏈，若存在則求之。

七、自選一個算法求貨郎擔問題。

八、給定帶權連通簡單圖的邊及權列表，輸入圖中兩個頂點，求兩點是否可達？若可達距離為多少？並輸出這條最短的鏈。

提示：

可以使用Dijkstra算法——迪傑斯特拉算法）

九、給定無向圖的邊列表，對該圖進行著色，求著色數。

十、輸入一個加權無向簡單圖的邊及權列表，求最小生成樹，以及這棵最小生成樹的權。

十一、輸入一段文章，全部用小寫字母，求各字母的哈夫曼編碼。

十二、要給n個人分配m個資源，輸入每個人可以獲得的資源情況，求最大匹配，

要求所有資源在滿足儘可能多的人獲得的情況下，全部分配出去。

論證

論題

有向無迴路圖又稱為dag。對這種有向無迴路圖的拓撲排序的結果為該圖所有頂點的一個線性序列，滿足如果G包含(u,v)，則在序列中u出現在v之前（如果圖是有迴路的就不可能存在這樣的線性序列）。一個圖的拓撲排序可以看成是圖的所有頂點沿水平線排成的一個序列，使得所有的有向邊均從左指向右。因此，拓撲排序不同於通常意義上對於線性表的排序。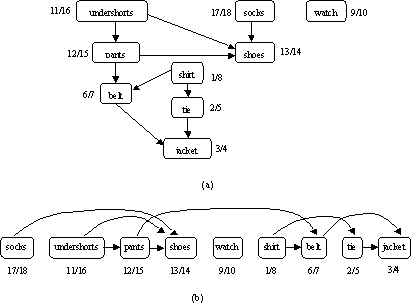

有向無迴路圖

有向無迴路圖經常用於說明事件發生的先後次序，圖1給出一個實例說明早晨穿衣的過程。必須先穿某一衣物才能再穿其他衣物（如先穿襪子後穿鞋），也有一些衣物可以按任意次序穿戴（如襪子和短褲）。

圖中說明經拓撲排序的結點以與其完成時刻相反的順序出現。因為深度優先搜尋的運行時間為θ(V+E)，每一個v中結點插入鍊表需占用的時間為θ(1)，因此進行拓撲排序的運行時間θ(V+E)。

為了證明算法的正確性，我們運用了下面有關有向無迴路圖的重要引理。

引理1

有向圖G無迴路若且唯若對G進行深度優先搜尋沒有得到反向邊。

證明：→：假設有一條反向邊(u,v)，那么在深度優先森林中結點v必為結點u的祖先，因此G中從v到u必存在一通路，這一通路和邊(u,v)構成一個迴路。

←：假設G中包含一迴路C，我們證明對G的深度優先搜尋將產生一條反向邊。設v是迴路C中第一個被發現的結點且邊(u,v)是C中的優先邊，在時刻d[v]從v到u存在一條由白色結點組成的通路，根據白色路徑定理可知在深度優先森林中結點u必是結點v的後裔，因而(u,v)是一條反向邊。（證畢）

定理1

Topological_Sort(G)算法可產生有向無迴路圖G的拓撲排序

證明

假設對一已知有問無迴路圖G=(V,E)運行過程DFS以確定其結點的完成時刻。那么只要證明對任一對不同結點u,v∈V，若G中存在一條從u到v的有向邊，則f[v]<F[U]即可。考慮過程DFS(G)所探尋的任何邊(U,V)，當探尋到該邊時，結點V不可能為灰色，否則V將成為U的祖先，(U,V)將是一條反向邊，和引理1矛盾。

因此，v必定是白色或黑色結點。若v是白色，它就成為u的後裔，因此f[v]<F[U]。若V是黑色，同樣F[V]<F[U]。這樣一來對於圖中任意邊(U,V)，都有F[V]<F[U]，從而定理得證。（證畢）

教材

我想很多學習圖論的人都知道J.A. Bondy和U.S.R. Murty著的《Graph Theory with Application》(Elsevier,1976)是圖論教材中的經典，時至今日，仍不失為初學者較好的入門書。還記得蘭州交通大學的張忠輔教授說過，國內第一屆圖論學會就是把大家集中起來學習邦迪的《Graph Theory with Application》，由此可見這本書對國內圖論屆的影響是如此之大。吳望名等人將其譯成中文版本《圖論及其套用》（北京：科學出版社，1984），1988年張克民等人編寫了該書的參考答案《圖論及其套用習題解答》（清華大學出版社，1988）。

在2008年J.A. Bondy和U.S.R. Murty出了新書《Graph Theory》(GTM 244, Springer, 2008), 大家可不妨將其看成是《Graph Theory with Application》的第二版，這本書在內容上做了重新調整，畢竟在第一版出版後的近30年裡湧現出了很多新的結果，所以《Graph Theory》在內容上加進了一些新的結果，這本書我只是讀了其中的幾章，覺得寫的非常棒，建議大家能夠讀讀，這裡也值得一提的是將第一版最後提出的50個問題進行了更新，並補充了一些新的問題。總之，我個人認為，《Graph Theory》的確是一部很優秀的圖論教材。

中國科學技術大學出版社出版的《圖論及其算法》，融有向圖和無向圖為一整體，系統地闡述了圖論的基本概念、理論、方法及其算法，內容包括圖的基本概念、Euler圖與Hamilton圖、圖論算法、樹及其套用、平面圖、獨立集與匹配、網路流和Petri網。 書中附有大量例題和習題，而且大部分習題有詳細解答。 該書選材精煉全面，內容處理恰當且有新意，立論嚴謹，敘述條理清晰，語言流暢。 該書可用作高校計算機、電子、信息、管理、數學等專業本科生必修課教材，也可供相關專業的研究人員、教師及圖論工作者參考。

實際套用

圖論算法是我們經常用來求解實際問題的一種方法，在數學建模的求解過程中也經常套用