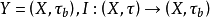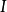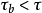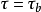囿空間(bornologic space)是一類局部凸空間,設E是局部凸空間,如果E中每個均衡凸的囿集都是零元的鄰域,則稱E是囿空間或有界型空間。局部凸空間是囿的,若且唯若在每個有界集上有界的半範數是連續的。設E是囿空間,E1是局部凸空間,則由E到E1的有界線性映射必是連續的。
基本介紹
- 中文名:囿空間
- 外文名:bornologic space
- 別稱:有界型空間
- 所屬學科:數學
- 所屬問題:泛函分析(拓撲線性空間)
基本介紹,相關定理,
基本介紹
註:定義就是說,若 ,且
,且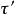 有界集與
有界集與 有界集一致,則
有界集一致,則 。
。

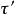


定理1 若 是局部凸空間,則下列等價;
是局部凸空間,則下列等價;

(1) X是囿空間;
(3) 任何在 有界集上取值有界的半范是連續的。
有界集上取值有界的半范是連續的。

證明:① 若X是囿空間,且V是吸收任意 有界集的凸集,若V不是0點
有界集的凸集,若V不是0點 鄰域,則在0點
鄰域,則在0點 鄰域子基中補上
鄰域子基中補上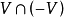 得到集
得到集 ,以
,以 為0點鄰域子基得到新的局部凸拓撲
為0點鄰域子基得到新的局部凸拓撲 ,顯然
,顯然 嚴格強於
嚴格強於 ,且
,且 與
與 有同樣的有界集,這與囿空間定義矛盾,故(1)
有同樣的有界集,這與囿空間定義矛盾,故(1)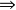 (2)。
(2)。



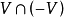







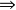
② 若X不是囿空間,則在X中可引入局部凸拓撲 ,使
,使 嚴格強於
嚴格強於 ,且
,且 與
與 有同樣的有界集,從而必存在0點
有同樣的有界集,從而必存在0點 鄰域,它不是0點
鄰域,它不是0點 鄰域,故(2)
鄰域,故(2)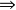 (1)。
(1)。







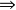
③ 若X中吸收任意 有界集的凸集是0點
有界集的凸集是0點 鄰域,又A是
鄰域,又A是 有界的。p是X的半范,且當
有界的。p是X的半范,且當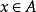 時有
時有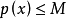 ,則
,則 。從而
。從而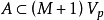 ,故
,故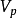 吸收任意有界集,因此
吸收任意有界集,因此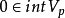 ,故p是連續的,所以(2)
,故p是連續的,所以(2)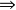 (3)。
(3)。



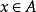
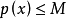

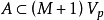
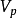
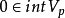
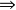
④ 若X不是囿空間,則存在局部凸拓撲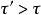 ,使
,使 與
與 有同樣的有界集,且存在一個凸的均衡吸收集V,它是
有同樣的有界集,且存在一個凸的均衡吸收集V,它是 的0點鄰域而不是
的0點鄰域而不是 的0點鄰域,故
的0點鄰域,故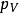 是在每個
是在每個 有界集上取值有界的半范,但
有界集上取值有界的半范,但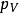 不是公連續的.故(3)專(1).口
不是公連續的.故(3)專(1).口
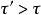




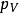

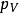
註:任給局部凸空間 ,我們在X上可以引入一個局部凸拓撲,稱為
,我們在X上可以引入一個局部凸拓撲,稱為 ,它是以吸收任何
,它是以吸收任何 有界集的一切凸集為0點局部基。容易看到,
有界集的一切凸集為0點局部基。容易看到, 是囿空間,
是囿空間, 有界集與
有界集與 有界集是一致的,且
有界集是一致的,且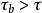 。
。






相關定理
定理2 任何賦可列半范的局部凸空間是囿空間,特別地,賦范空間是囿空間。
證明:不妨設

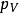
對X中任何有界集E,由於V吸收E,故有

但由於V不是0點鄰域,故對任何正整數n及 ,有
,有 ⊄
⊄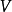 ,,從而存在
,,從而存在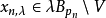 ,所以,
,所以, ,但
,但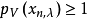 ,令
,令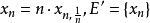 ,當
,當 時,由(1),
時,由(1),


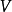
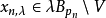

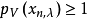
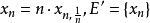


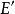
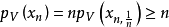

定理3 設 是局部凸空間,則X是囿空間若且唯若從X到任意局部凸空間Y的線性有界運算元是連續的。
是局部凸空間,則X是囿空間若且唯若從X到任意局部凸空間Y的線性有界運算元是連續的。

證明:設X是囿空間,Y是局部凸空間, 是線性有界運算元(有界指將有界集映成有界集)。設W是Y的0點凸鄰域,則
是線性有界運算元(有界指將有界集映成有界集)。設W是Y的0點凸鄰域,則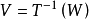 是X中凸集,且吸收X中任意有界集(事實上,設E是X中有界集,則
是X中凸集,且吸收X中任意有界集(事實上,設E是X中有界集,則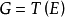 是Y中有界集,故存在
是Y中有界集,故存在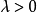 ,使
,使 ,故
,故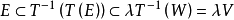 ),由於X是囿空間,故V是0點領域,從而T是連續的。
),由於X是囿空間,故V是0點領域,從而T是連續的。

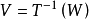
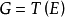
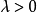

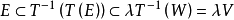
推論1若X是囿空間,則X上的每個有界線性泛函必是連續的。
推論2 若X是Banach空間,Y是局部凸空間,則任何有界線性運算元 必是連續的。
必是連續的。