單變數統計分析是對某一變數的數量特徵所進行的描述和推論,它是最簡單也是最基本的統計。包括兩個大的方面,即描述統計和推論統計。
基本介紹
- 中文名:單變數統計分析
- 外文名:Single variable statistical analysis
- 所屬學科:數學(統計學)
- 內容:描述統計和推論統計
- 相關概念:標準差、置信度、四分位差等
基本介紹
單變數描述統計
集中趨勢分析


離散趨勢分析



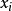

單變數推論統計
區間估計



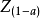






單變數統計分析是對某一變數的數量特徵所進行的描述和推論,它是最簡單也是最基本的統計。包括兩個大的方面,即描述統計和推論統計。





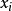




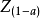





單變數統計分析是對某一變數的數量特徵所進行的描述和推論,它是最簡單也是最基本的統計。包括兩個大的方面,即描述統計和推論統計。...
單變數分析主要集中在單變數的描述和統計推斷兩個方面,在於用最簡單的概括形式反映出大量樣本資料所容納的基本信息,描述樣本數據中的集中或離散趨勢,單變數統計推斷則...
多變數分析(multivariable analysis)為統計方法的一種,包含了許多的方法,最基本的為單變數,再延伸出來的多變數分析。統計資料中有多個變數(或稱因素、指標)同時存在...
第三節 統計調查方案和組織形式第四節 統計數據的整理與顯示思考與練習第三章 單變數統計描述分析第一節 集中趨勢分析第二節 離散趨勢分析...
《時間序列分析:單變數和多變數方法(第2版)》不僅對單變數與多變數時間序列的時域和頻域分析提供了一個全面介紹,而且在書中包含了許多單變數和多變數時問序列模型...
數據,《社會統計學:對問卷調查數據的統計分析》主要介紹對問卷調查數據進行統計分析的基本原理與方法,其內容涉及單變數分析、雙變數分析和簡單的多變數分析(詳盡分析)...
《統計數據分析基礎教程》是中國人民大學出版社出版的一本書。...... 數據基本統計分析(單變數的頻率分析、雙變數的交叉表分析、多選變數的頻率分析、描述統計分析)...
多元分析是研究多個自變數與因變數相互關係的一組統計理論和方法。又稱多變數分析。多元分析是單變數統計方法的發展和推廣。...
分析、比較分析、因素分析及多種分析方法,對企業的經營活動、財務活動等進行分析...單變數預警模型 .智庫 詞條標籤: 科學 V百科往期回顧 詞條統計 瀏覽次數:次 ...
《Excel套用與數據統計分析》是2011年暨南大學出版社出版的圖書,作者是王斌會。...... 以及數據透視表、模擬運算表、單變數求解X-具和規劃求解工具等數據分析工具的...
因素分析法是利用統計指數體系分析現象總變動中各個因素影響程度的一種統計分析方法...傳統的單變數和雙變數分析往往在信息的處理上要么失去有用的信息,要么引入無用...
《SPSS統計分析方法及套用》是薛薇主編,由電子工業出版社於2009年出版的一本圖書...7.1.3單樣本K?S檢驗7.1.4變數值隨機性檢驗7.2兩獨立樣本的非參數檢驗...
《Excel統計分析基礎教程》是2011年8月1日清華大學出版社出版的圖書,作者是黃昆...3.5.1 單變數分組3.5.2 組距分組3.6 圖表製作3.6.1 基本方法3.6.2 Excel製圖...
現代統計分析方法是處理多維數據的重要工具,全書共12章:矩陣理論、隨機向量、正...12.5.1 單變數方差分析 29812.5.2 多變數方差分析 30212.5.3 重複測量的...
《SPSS在統計分析中的套用》是2007年清華大學出版社出版的圖書,作者是朱建平等。...... 第6章方差分析 566.1方差分析概述 566.2單因素單變數方差分析 56...
《SPSS數據統計與分析套用教程:基礎篇》是一本於2017年1月1日清華大學出版社...16.2.1單變數描述 34716.2.2變數關聯探索 34916.3對因變數變換後的建模...
《套用商務統計分析》是2007年北京大學出版社出版的圖書,作者是王漢生。...... 本書是以實際案例驅動的套用統計學教材,包括線性回歸、方差分析、協方差分析、0-1變...
《統計數據分析基礎教程習題與實驗指導》是中國人民大學出版社出版的教材《統計...實驗3.4 在SPSS中定義變數第4章 單變數的頻率分析4.1 本章習題...
《SPSS統計分析實例精選》是由蔡建瓊,於惠芳,朱志洪編寫,清華大學出版社出版的一...7.2 繪製單變數的頻率表7.3 進一步通過TABLE過程繪製多變數的頻率表...
內容包括Minitab的基礎知識、基本統計量、統計表和列聯表資料的檢驗、方差分析、等效檢驗、非參數檢驗、回歸分析、可靠性/生存分析、多變數分析、時間序列分析、功效...
本書共分為17章,為讀者詳細講解了Excel在統計分析中的套用,內容包括Excel 2013...13.1.1 單變數模擬運算表 19813.1.2 雙變數模擬運算表 199...
《北京大學光華管理學院教材商務統計系列套用商務統計分析》是以實際案例驅動的套用統計學教材,包括線性回歸、方差分析、協方差分析、0-1變數回歸、定序回歸、泊松回歸...
《多變數分析:SPSS的操作與套用》,北京大學出版社出版的圖書,作者是林震岩。...... 第四章 單變數描述性分析第一節 描述性統計原理第二節 報告第三節 描述性...
