基本介紹
- 中文名:單向方差分析
- 外文名:One-Way analysis of variance;One-Way ANOVA
- 別名:單因子方差分析、F-檢驗或F-比值
- 所屬學科:數學(統計學)
- 簡介:最簡單的方差分析方法
- 相關概念:總方差、組間方差和組內方差
- 提出者:菲希爾(R.A.Fisher)等
單向方差分析的基本概念
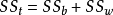






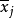








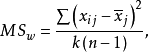



Scheffe檢驗
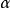







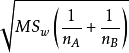


套用舉例




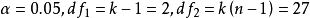







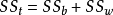






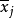








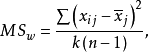



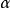







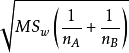






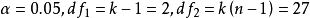






單向方差分析亦稱單因子方差分析、F-檢驗或F-比值,是由菲希爾(R.A.Fisher)和他的英國同事開發的。這個檢驗以Fisher的第一個字母命名。當有三個或更多個獨立組和...
雙向方差分析(two way analysis of variance),簡稱ANOVA,是指用於分析兩因素實驗資料的方差分析。在統計學中,雙向方差分析(ANOVA)是單向方差分析的延伸,它檢驗兩個...
秩方差分析是基於秩的多個樣本齊一性的非參數統計檢驗方法,與方差分析法類似。例如,檢驗多個獨立樣本齊一性的“克魯斯卡爾- 沃利斯檢驗”,亦稱做“克魯斯卡爾-...
組內方差指方差分析中的隨機誤差的方差。 在方差分析模型中,觀測值方差的各個分量為方差分量,方差分量的概念是針對含隨機效應的方差分析模型引進的,因此稱這樣的...
4.2 單向分組方差分析4.3 多種處理的單向分組方差分析4.4 多項式比較4.5 完全隨機設計第5章 區組結構5.1 完全隨機設計5.2 隨機區組設計...
一般平均亦稱總平均(Grang Mean ),是方差分析中回響變數觀測值的數學期望,等於各工程平均的簡單或加權算術平均值,其無偏估計量是全部觀測值的總平均值。...
對於採用完全隨機化設計的實驗,其數據的分析方法就是所謂單向方差分析。取這樣的名稱是由於我們僅僅根據一個準則,即實驗單元所屬的一組處理來對實驗單元(從而對所...
第七章 方差分析7.1 方差分析的基本原理7.2 單向方差分析7.2.1 單向方差分析的基本概念……第八章 線性回歸分析第九章 因子分析...
第三節等級方差分析一、克一瓦氏單向方差分析 ( 完全隨機設計 )二、弗里德曼雙向等級方差分析第四節非參數相關 ―― 列聯相關 (Contingency Correlation)第五節 ...
10.5 單向方差分析第11章 X2檢驗11.1 兩個比例差異的X2檢驗11.2 多個比例差異的x2檢驗11.3 獨立性的X2檢驗第12章 一元線性回歸...
第二節 符號秩次檢驗第三節 克一瓦氏單向方差分析第四節 弗里德曼雙向方差分析參考文獻附錄後記參考資料 1. 心理與教育統計學 .豆瓣[引用日期2017-09-20] ...
4.6.6 克一瓦氏單向方差分析4.6.7 弗里德曼方差分析4.6.8 獨立樣本和相關樣本t檢驗4.6.9 方差分析4.6..0 報告ANOVA時的注意事項...
13.1 方差分析方法13.2 試驗設計13.3 單向方差分析:完全隨機設計(單向ANOVA)13.4 方差齊次性檢驗13.5 單自由度的比較13.6 多重比較...
五、DOE結果分析 1、因素影響與互動影響 2、極差分析 3、ANOVA方差分析 單向方差分析 雙向方差分析 4、回歸分析 六、如何利用Minitab進行DOE分析 1、在Minitab中...
在第14章和第15章的單向方差分析中,討論了影響t檢驗檢驗力的因素。在第14章中,介紹了檢驗影響自變數置信區間的方法和傳統的假設檢驗方法。...
第五節單向方差分析(One-Way ANOVA) 第九章一般線性模型(General Linear Model) 第一節一般線性模型單變數分析的基本過程 第二節完全隨機設計資料的方差分析 ...
§9.1 方差分析的必要性和方差的加和性§9.2 單向方差分析§9.2.1 完全隨機化設計§9.2.2 多重比較方法§9.2.3 樣本容量和模型效應不同的單因素方差分析...
