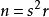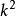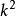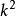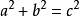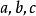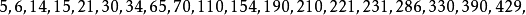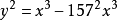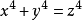同餘數

同餘數是一個三條邊均為有理數的直角三角形的面積。換一種說法，如果有三個正有理數x,y,z，滿足條件x²+y²=z²，1/2xy=N，則N為同餘數。若正整數N是同餘數，則N稱為整同餘數。

同餘數問題是“尋求一個簡單的判別法則來決定一個自然數n是否是同餘數”。如何判斷和尋找同餘數是一個幾千年的問題，這也與最前沿的數論研究有深刻關係。

基本介紹

• 中文名：同餘數
• 外文名：congruent number
• 含義：是邊均為有理數的三角形的面積
• 條件：N是同餘數，x2+y2=z2，N=1/2xy
• 意義：三大千年數論難題之一
• 學科：數學

定義

叫同餘數，如果它是三邊邊長都是有理數的直角三角形的面積。用式子來表示就是：如果存在三個正有理數 滿足 和面積 ，此數 就稱為同餘數。

例如：6是同餘數,因為它是三邊邊長3、4、5的直角三角形的面積。5也是同餘數，因為它是邊長為 的直角三角形的面積。

整同餘數

如果正整數n是同餘數，那么，n稱為整同餘數。

設n是正有理數，且對 ，這裡s是正有理數，而r是無平方因子的正整數，那么n是同餘數若且唯若r是同餘數。

由此可見，同餘數的問題可轉化為整同餘數來處理。

本原同餘數

如果一個A 是不含平方因子的整同餘數，則 A 稱為本原同餘數。

重要結論

定理：n是整同餘數的充要條件是存在正整數a,b,v，使得：

其中， 是正整數，一奇數一偶數

推論：若不定方程 沒有正整數解，則n不是同餘數。

套用舉例

例1 試證明：1不是同餘數

證明：因為不定方程沒有正整數解，由推論知，1不是同餘數。

例2 試證7是同餘數

證明：在中，取 ，得，故7是同餘數

例3 設k為正整數，試證不是同餘數

證明：假設是同餘數，則有：有正整數解，從而，不定方程有正整數解，但不定方程沒有正整數解，矛盾，故假設不成立。因此，不是同餘數

歷史

同餘數問題在數學界被稱為三大千年數論難題之一（另外兩個是完全數問題與三次和三次以上丟番圖方程有解問題）。古阿拉伯人是通過研究直角三角形的面積提出同餘數問題的。對於直角三角形，人們已經知道，它的三邊滿足方程 ，這就是我們所說的的勾股定理（在國外又被稱為畢達哥拉斯定理）。當直角三角形的三邊 為有理數，若直角三角形的面積 為正整數，這樣的 就是古阿拉伯人所欲求得的同餘數。

早在一千多年前的一份阿拉伯手稿中，提出了這樣一個問題：一個正整數n何時能成為一個一個由三個有理平方數形成的等差數列的公差，也就是說 都是平方數。這與前面的定義是等價的，因為 形成我們想要的等差數列。反過來，若 ，則 形成一個面積為 的有理直角三角形。這便是同餘數名稱的由來。容易看出，乘上一個平方數不影響一個數是否成為同餘數。所以人們常常假設n不含平方因子。在阿拉伯人的手稿中，給出了34個同餘數，其中，不含平方因子的有30個：

以後的古希臘人，也曾在同餘數問題上得到了一些具體的結果。

研究成果

經典結果

到了十七世紀，法國大數學家費爾馬開始對同餘數問題進行系統地研究，首先，他把古阿拉伯人的研究方法改造為一個定理：正整數n是同餘數若且唯若方程組 具有y≠0的整數解。這就使初等數論理論開始套用到同餘數問題的研究之中，運用他自己發明的無窮遞降法，費爾馬證明了1 ，2 ，3 不是同餘數。其中1不是同餘數等價於方冪等於4的費馬大定理，即 沒有整數解。這也是最早出現的對非同餘數的研究成果。萊昂哈德·歐拉(Euler)第一個證明了7是同餘數。

公元972年，在一份阿拉伯手稿中，提出了這樣一個問題：一個正整數n何時能成為一個一個由三個有理平方數形成的等差數列的公差，也就是說x-n,x,x+n都是平方數。

十三世紀，義大利數學家斐波那契指出5和7是同餘數，他也猜想1、2、3不是同餘數，但未能給出證明。

直到1659年，法國大數學家費爾馬運用他自己發明的無窮下降法證明了1、2、3不是同餘數。

十八世紀，大數學家歐拉首次證明了7是同餘數。

1952年，Heegner證明了任意模8餘5、7的素數和任意模4餘3的素數的兩倍均為同餘數。

2000年，美國克雷數學研究所公布了千禧年七大數學難題，每破解其中一個難題者將獲得100萬美元的獎金。其中就有著名的BSD猜想（全稱Birch and Swinnerton-Dyer猜想），而這個猜想與同餘數問題有緊密的聯繫。

2012年，田野證明了存在無窮多個具有任意指定素因子個數的同餘數，這是在同餘數問題上的一個根本性突破，也首次給出了解決BSD猜想的線索。

與橢圓曲線關係

近代人們發現同餘數問題與橢圓曲線緊密相關。n是同餘數等價於橢圓曲線 有無窮多個有理點。特別的，在假設BSD猜想前提下，模8餘5，6，7的n是同餘數。

把這個定理與橢圓曲線理論相聯繫，使人們對同餘數問題的研究有了重大的進展，不過人們同時也發現，用這個定理去求解一個具體的同餘數仍然非常地困難。例如，人們已知157是同餘數，但在方程 的最小解 中，x的分母和分子都近100位，它對應的直角三角形的斜邊為

.

猜想性的判定法則

Tunnell證明了在假設BSD猜想的前提下，若n是奇數，定義

若n是偶數，定義

則n是同餘數等價於a(n)=0。由於解析秩為0的情形已經被證明，因此a(n)不等於0能推出n不是同餘數。利用這種方法，可以有效地驗證一個非同餘數。

2下降法

在非同餘數方面，人們推廣了費馬的方法，證明了任何素數或者素數的兩倍，如果模8餘1，2，3，是非同餘數。馮克勤證明了對任意的k>0，存在無限多個非同餘數恰好有k個素因子。

與特殊值公式的關係

利用特殊值的導數公式，Heegner證明了模8餘5，6，7的素數或素數兩倍是同餘數。在此基礎上，田野證明了對任意的k>0，存在無限多個非同餘數恰好有k個素因子。

50%-50%猜想

人們猜想，幾乎所有的模8餘5,6,7的平方自由的正整數對應的橢圓曲線秩為1，幾乎所有的模8餘1,2,3的平方自由的正整數對應的橢圓曲線秩為0。也就是說所有的同餘橢圓曲線中有50%秩為0，50%秩為1。田野首次證明了秩為0和秩為1的百分比均大於0，相關文章尚未發表。