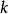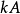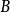基本介紹
- 中文名:可公度量
- 外文名:commensurable quantities
- 別名:可通約量
- 所屬學科:數學
- 所屬問題:初等代數
基本介紹,相關分析,相關定理,
基本介紹
作線段度量時,如果兩條線段都能用第三條線段量盡,即兩條線段都是第三條線段的整數倍,則把第三條線段稱為前兩條線段的一個公度,這兩條線段就叫做可公度量(或可通約量),由於公度的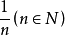 仍是一個公度,可知沒有最小的公度,但公度顯然不會超過兩條線段中的較小者,故公度中必有最大者,稱為最大公度。
仍是一個公度,可知沒有最小的公度,但公度顯然不會超過兩條線段中的較小者,故公度中必有最大者,稱為最大公度。
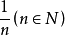
相關分析
假設A、B 是可通約的兩個量,它們的比 是既約分數。用
是既約分數。用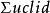 輾轉相除法求m與n的最高公因數,結果一定是1。如果兩個量可通約,那么輾轉相度一定有量完的時候。這時候充當除數的那個量就是公度(common measure);
輾轉相除法求m與n的最高公因數,結果一定是1。如果兩個量可通約,那么輾轉相度一定有量完的時候。這時候充當除數的那個量就是公度(common measure);

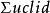
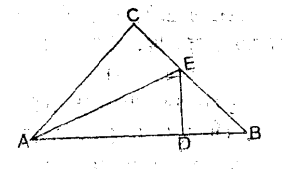 圖1
圖1反過來,若是輾轉相度永不停止,那么這兩個量就是叵通約的。例如等腰直角三角形ABC中,弦AB與股AC就沒有公度。這因為在AB上取AD=AC,又作AE平分∠BAC 交BC 於E,這時
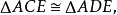
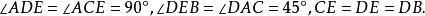
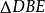
當我們以AC度AB時,量一次剩下DB。以DB度AC和以DB度BC一樣,量一次剩下BE。下邊雖說可以再量,然而DB與BE互度時,工作的實質毫不減於AC與AB的互度。可見這項互度工作永遠不能休止,由此知道這是不可度的。
相關定理
定理一 設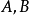 可通約,
可通約,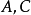 可通約,則
可通約,則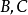 可通約。
可通約。
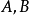
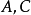
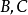
定理二 設量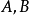 可通約,那么
可通約,那么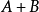 與
與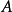 是可通約量,
是可通約量,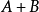 與
與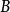 也是可通約量。
也是可通約量。
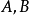
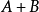
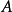
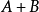
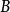
證明:根據假設:
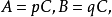
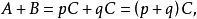
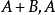
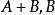
定理三設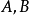 是可通約量,而且
是可通約量,而且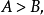 則
則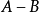 與
與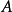 ,
,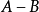 與
與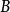 也各是可通約量。
也各是可通約量。
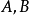
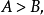
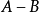
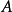
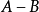
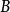
證明: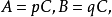 所以
所以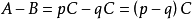 。由此即得
。由此即得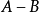 與
與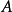 是可通約量,同理可證
是可通約量,同理可證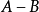 與
與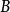 也是。
也是。
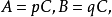
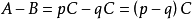
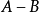
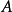
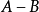
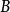
定理四 設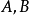 是可通約量,
是可通約量,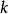 是任何自然數或分數,那么,
是任何自然數或分數,那么,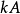 和
和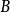 是可通約量。
是可通約量。