1.1 原子核中的結團現象,1.1.1 早期的研究,1.1.2 對稱性和諧振子,1.1.3 原子核分子,1.1.4 結團的形狀,1.2 實驗研究進展,1.3 理論研究進展,1.3.1 微觀結團模型概述,1.3.2 費米分子動力學模型,1.3.3 有效液滴模型,1.3.4 密度依賴的結團模型,1.3.5 協變密度泛函理論,
1.1 原子核中的結團現象 原子核是一個有限的量子多體系統,它由質子和中子兩種核子組成,核子間通過核力發生相互作用。基態的原子核具有殼結構,核子在類似原子系統的平均場中獨立運動。殼結構、單粒子激發和集體運動是原子核系統中的三個方面。另外,原子核系統具有與原子系統不同的特性。最大的不同是,原子核是通過核力的吸引形成自束縛系統。由於吸引作用,核子的空間關聯非常強,因此,出現了不同形式的核子聚集和發散。此外,原子核系統的飽和性,即單核子結合能和核心密度幾乎為常數,與質量數無關,這意味著在很小的激發能作用下,核子就能夠發生聚集和分散。因此,原子核的特性促使原子核形成結團結構,即原子核由幾個結團和受束縛的核子組成。核子的聚集和分散一直持續到高激發能,中能重離子碰撞產生的大量結團和碎片核的激發能完全可以同原子核的結合能大小相提並論。
原子核的結構傳統表述為質子和中子大致均勻分布。然而,即使在原子核科學的初期,人們就知道,核子的聚集(原子核的結團結構)對於描述輕核區核素的結構極其重要。在許多情況下,存在一個更加恰當的原子核圖像,如圖1.1所示。
圖1.1 ^{16}O的4α結團結構 物理情景中反對聚集的物理圖像一直存在。反對聚集必然會導致勢能的明顯減小或者增加核素的穩定性。通過對2dF 銀河系紅移的研究表明,物質聚集成了細絲狀的結構。這種聚集結構是由宇宙大爆炸的不均勻性發展而來。星球聚集形成星系或太陽系中行星受到太陽引力的束縛,尺度進一步減小,更加結團化。原子在氣體相或液體相中形成分子,在固體相中形成晶體。強子內部的夸克相互約束,組成的夸克種類為一個特別的數字。因此,如果這種現象不能擴展到原子核領域,那將會令人震驚。輕核的結構在很大程度上受結團的影響。α 粒子結團在具有相同質子數和中子數的偶A核中最常見。豐中子核靠近衰變閾值時,會出現分子類結構,價中子在 α 粒子間不斷交換。最大的挑戰是可能形成三個中心的分子,甚至是更複雜的結構。位於中子滴線的原子核的穩定性限制只能通過最輕的核進行探測。原子核的結團核心周圍存在中子云,稱為中子暈,這是結團的一種形式。中子滴線的核素可能具有更多普遍的形式,即核心形成結團,結團周圍環繞著價中子海,價中子(紅色)在核心(藍色)的周圍不斷交換,如圖1.2所示。
圖1.2 中子滴線核易形成結團 1.1.1 早期的研究 重核的α衰變讓人們意識到,核子的結團結構(兩個質子和兩個中子)可能在衰變之前早已形成。如果需要檢驗輕核的基態性質,即單核子結合能(BE/A)在具有相同質子數和中子數的偶A核處出現了最大值(例如He, Be, C.....),(見圖1.3)。(圖1.3 輕元素的單核子結合能。同一種顏色的線條表示相同的元素。同位素鏈中單核子結合能為最大值的核素是具有相同質子數和中子數的偶A核。) 更重要的是,這些核素都能看作由α粒子組成。事實上這個結論是在原子核早期的模型的基礎上進行擴展得到的,就這一點而言,Hafstad 和Teller的工作是很有創意的。對A=4n(n=2,3,4,...) ,
N =
Z 的核素的結合能進行分析可知,核素的結合能與α粒子的結合方式成線性關係(圖1.4),表明α結團在原子核的基態中扮演重要角色。(圖1.4 (上圖) 結合能與可能的α粒子結合種類的關係。對於
8 Be只有一種結合方式,
12 C有3種,
16 O有6種等等。(下圖) 已經提出的α粒子分布。)
圖1.3 輕元素的單核子結合能 圖1.4 (上) 結合能,(下) α粒子分布。 儘管這種圖像過於簡單,但本質上是正確的,尤其是當結團的衰變閾值(即原子核分開形成結團結構的Q值)位於靠近基態的位置。許多的原子核的基態不存在分割開的α粒子結團結構,而是結合得更加緊密,同時出現結團的重疊(這是由於受泡利不相容原理的影響)。然而,這種對稱性在早期的結團圖像中的確存在。20世紀50年代,日本的Morinaga提出了一個十分極端的預言,α粒子的分布可能為直線型。這個觀點說明基態的結團結構不應該很明顯,但是隨著原子核內能的增加會出現結團結構。一個原子核出現結團結構是完全允許的。類似地,當原子核分裂成結團的時候,對應產生的能量可由未分裂成結團的核子和形成結團核子的質量差計算得到。由此,核素的結合能在靠近或者低於結團衰變閾值時,結團結構可能十分明顯。
關於靠近衰變閾值處的結團態的研究變得非常重要,詳細情況可以參見Ikeda圖(圖1.5)。由圖1.5可知,與衰變閾值相同的激發態,更加容易觀察到結團結構。因此,雙α結團結構能夠在Be的基態找到,
8 Be衰變到兩個α粒子的時間約為10
-16 秒。3α結團結構可能更加靠近3α衰變閾值,即7.27MeV。眾所周知,
12 C的7.65MeV的Hoyle態存在明顯的3α結團結構。Brink 使用α結團模型研究類α粒子系統的穩定結構和近似穩定結構。他提出了大量的幾何學的或者晶體狀的類α粒子原子核的形狀結構。儘管這種結構與激發態有關,但是該結論在許多方面與早期的預言是一致的。
圖1.5 Ikeda圖 1.1.2 對稱性和諧振子 Ikeda圖表明,結團結構的出現與原子核的激發能關係密切,結團結構多出現在衰變閾值附近。同時對稱性有利於結團的形成,這是Hafstad 和Teller預言的關鍵點。原子核的殼模型能夠對原子核的單粒子運動進行很好的描述,該模型假設核子在一個平均場中運動,該平均場表述為,一個核子受到其它所有核子相互作用的平均。然而,殼模型中核子的平均自由程明顯大於原子核的尺度。球對稱諧振子能夠對許多輕核系統進行很好描述,但是在很輕的系統中,形變在原子核的結構中扮演重要角色,核子運動的簡單特徵可以通過形變諧振子得到(圖1.6),能級由
E=hω ⊥ n
⊥ /(2π)+
hω z n
z /(2π)+16
hω 0 /π給出。其中,垂直(⊥)和平行(
z )於形變軸的振動特徵頻率是必須的,相應的約束條件為
ω 0 =2
ω ⊥ +
ω z ,四極形變為ε=ε
2 =(
ω ⊥ -
ω z )/
ω 0 (見圖1.6)。如果ε為正,這意味著原子核發生長橢形變(類似橄欖球);當ε為負,原子核發生扁橢形變(類似南瓜);ε為零時,原子核為球形。
圖1.6 形變諧振子的能級 表1.1 與形變有關的結團結構和新幻數的關係
形變的幻數
球形幻數
球形的結團組成
N
超形變,二聚物結構
4
2 + 2
α +α
10
8 + 2
16 O+α
16
8 + 8
16 O+16 O
28
8 + 20
16 O+40 Ca
N
巨超形變, 鏈式結構
6
2 + 2 + 2
α +α +α
12
2 + 8 + 2
α +16 O+α
24
8 + 8 + 8
16 O+16 O+16 O
36
8 + 20 + 8
16 O+40 Ca+16 O
48
20 + 8 + 20
40 Ca+16 O+40 Ca
60
20 + 20 + 20
40 Ca+40 Ca+40 Ca
N
扁橢原子核, 薄煎餅形狀
8
6+2
12 C+α
12
6 + 6
12 C+12 C
18
12 + 6
24 Mg+12 C
24
12 + 12
24 Mg+24 Mg
形變為零時,諧振子的解產生一系列簡併度(2,6,12,20…),即原子核中有多少個質子和中子能夠占據軌道。當勢場是形變的,與振動相關的能級能量沿著形變軸不斷減小(振動頻率也不斷減小),然而垂直於形變軸的能量不斷增加。例如,2:1 和3:1的形變時,會出現一系列的能級交錯,從而導致一系列的殼能隙。值得一提的是,2:1時的球形簡併出現過兩次(即2, 2, 6, 6, 12, 12...),3:1時的球形簡併出現過三次。使用形變諧振子時。這種對稱性表明2:1形變時存在雙結團,3:1形變時存在三結團。Rae等用形變的結團結構來理解新的幻數,如表1.1所示。超形變的原子核具有2:1的形變軸勢場,巨超形變的原子核具有3:1的形變軸勢場。
這種現象不僅能夠在簡併中觀察到,而且能從諧振子模型計算得到的密度分布得到。例如,圖1.7中對應的簡併模式為2+2, 2+2+2 和2+2+2+2對應的形變比例為2:1, 3:1和4:1。α結團結構在每種情形的密度分布圖中都十分明顯。儘管這個近似相對簡單,但是更複雜的計算表明,原子核結構具有相同的對稱性。
8 Be的ab從頭計算較好地描述了輕核中的結團結構,該模型中考慮三體力的自由核子-核子相互作用。由核子-核子相互作用力的相關性可得,
8 Be具有
α +
α 結團結構。
圖1.7 2:1 、3:1, 4:1形變軸的密度分布圖 諧振子是計算原子核結構性質的簡單近似,同時透露出潛在的對稱性。如果原子核的結構、結合能、激發能的細節能夠很好再現,那么採用更複雜的方法是必須的。更加複雜的方法包括:
(1)反對稱分子動力學(AMD):用有效的核子-核子相互作用的ab從頭計算近似;
(2)費米分子動力學(FMD):用張量相互作用的AMD方法;
(3)共振群方法(RGM)和生成坐標方法(GCM):統一描述核反應和結構的微觀方法(例如);
(4)Bloch–Brink結團模型:多中心的α結團模型;
(5)局域勢結團模型:採用結團中心勢的雙結團模型;
引人注目的是,所有的模型預言的結團結構種類都十分相似。
1.1.3 原子核分子 前面的結團結構主要在研究α結合核的形式是什麼,即什麼樣的核能夠分離成α粒子核。有趣的是,當存在額外的價核子(質子或中子),核子系統會出現什麼樣的新情景。最典型的價粒子是中子,它可能改變α粒子的核心,這種變化過程與由原子組成的分子中的電子交換過程類似。在原子系統中,電子的共價交換約束兩個質子形成氫氣分子;在原子核系統中,
9 Be的基態的兩個α粒子通過交換中子形成約束。原子核情形的共價軌道的本質與O
2 的軌道十分相近,其中分子軌道由p軌道的線性組合得到。
5 He中
α 粒子的兩個質子和兩個中子填在殼模型的1s
1/2 軌道,另一個中子位於p殼,對應的基態自旋和宇稱為3/2
- 。圖1.8表明,分子軌道的種類可能形成兩個
4 He的核心和價中子。(圖1.8 Be同位素鏈的分子軌道的形成。左圖中的紅色球體表示α粒子的位置,藍色的啞鈴狀區域的密度與分子軌道相關。中子軌道平行或垂直於間隔軸。p軌道的線性組合得到
π 和
σ 分子軌道(右邊兩圖)。)p軌道的空間對齊方式垂直或者平行於兩個α粒子的間隔軸。垂直代表
π 類分子軌道,平行代表
σ 類分子軌道。兩個α粒子通過交換中子進行約束,這是
9 Be穩定的原因。W. von Oertzen及其同事對原子核的分子結構進行了大量的研究。
圖1.8 Be同位素鏈的分子軌道的形成 圖1.9 ^{8}Be和^{9}Be的轉動帶 這個模型預言 9 Be的3/2- 基態對應π 類軌道,1/2+ 的低激發態對應 σ 類軌道。 9 Be的確存在Jπ =3/2- 的基態和1.68 MeV的1/2+ 低激發態。形變的分子結構實質表明,9 Be存在轉動行為,結果被實驗確認。從轉動帶能夠提取出兩種組態的轉動慣量,與分子解釋一致。實驗情景見圖1.9。基態的π 類轉動帶用實心圓圈標出。這個帶的形變由h2 /8π2 Θ等於0.525得到,這與8 Be的雙α系統類似h2 /8π2 Θ等於0.48。與σ 分子軌道相關的轉動帶存在由Corriolis去耦合引起的巨大效應。然而,實際上h2 /8π2 Θ得到的值為0.386,這意味著存在一個比π 組態更大的轉動慣量,可通過σ 軌道的本質進行理解,σ 軌道位於雙α粒子核心之間,會增大雙α間距。
類似的結構在其它的雙中心繫統中也能找到,例如10 Be和11 Be。核子系統的分子行為的很好證據:W. von Oertzen在研究氖同位素鏈時,發現α粒子的一個核心被16 O結團取代。的確,20 Ne (16 O+α )大量的反對稱結團結構在21 Ne和22 Ne的分子軌道行為中扮演著重要角色。大量的反對稱結構導致分子譜中的宇稱成對出現。α粒子和16 O的分子軌道是雜化軌道,由α粒子周圍的p軌道和16 O周圍的d軌道混合而成。(圖1.10 改進的Ikeda圖,圖中給出了分子結構和對應的激發能。)圖1.10表明改進的Ikeda圖表現出多種分子結構,許多在實驗上已經觀察到。大量不對稱的分子結構同樣出現在三個α粒子的系統中。例如,13 C中的三個α粒子線性排列,價中子位於核心α粒子和其它粒子之間,會產生大量的反對稱性。 20 Ne的兩個轉動帶具有相同的轉動慣量但宇稱相反。兩個轉動帶的能級劈裂代表中子隧穿到中心α粒子的幾率,對應的分子軌道如圖1.11a-c。人們對二聚物到三聚物的擴展分子結構的可能性進行了研究。這裡的中子可能在三個α粒子間交換。在兩個、三個和四個中心的原子核系統中,由p軌道線性結合形成的可能分子軌道例子見圖1.11(圖1.11 三個中心(a-c) 和四個中心(d-g) 的分子軌道。這些分子軌道由p態線性組合得到,排成一條線垂直於間隔的軸,並且具有π軌道特徵。能量最低的組態沿水平軸有最少的節點。黑色的點代表α粒子的中心。)。這裡中子可能會在N 箇中心交換。三個α粒子可能排列成線性或分解成為三角形分布,中子都會在三個中心之間改變位置。13 C 和14 C這種結構的實驗證據十分有限,但是更多的實驗數據是有必要的。16 C的最佳情形是線性排列,儘管實驗例子非常稀少。
1.1.4 結團的形狀 輕核中的結團結構出現在
N=Z 的核和豐中子核的基態或者激發態。不同的核有多種不同的結團構造,主要有線性鏈式結構,八極形變,三角形,環狀和花朵狀。
圖1.10 改進的Ikeda圖 Wuosmaa等的實驗研究激發了人們對奇特的α粒子鏈式結構的興趣,該實驗
12 C(
12 C
, 6α) 在
E c.m
. = 32
. 5MeV處觀察到了類共振結構。Chevallier等得到了
16 O具有4α鏈式態的實驗證據。長期以來,
12 C的
態的能量為7.65MeV,人們一直把它當作3α鏈式結構而稱為Hoyle態。人們把該態當做α粒子的玻色-愛因斯坦凝聚,認為所有的α粒子位於質心波函式的相對s態。靠近nα衰變閾值的α粒子態可能是A=4n核素的一般特徵。要想在普通的核反應中得到更長的鏈式結團是不可能的,但是在高激發的豐中子核物質中是可能的。錒類核的巨超形變也以結團結構的形式討論,可能具有八極形變結構。
36 Ar最可能的結團形變態為
12 C +
24 Mg 和
16 O +
20 Ne,均為八極形變的結構。三個核心的核可能形成三角形的結團結構,例如
14 C,見圖1.12(圖1.12
1 4 C的三角形結團結構,(a) 具有一個節點的中心價粒子波函式,;(b) 中心價核子波函式具有極大值,,虛線表示三個中心共享兩個價中子)。環狀的結團具有奇特的密度分布,中心密度不斷減小為零,超核中會更加常見。其產生機制可能是:重離子間的高能碰撞可能會導致低密度的快速轉動的核子剩餘,從而形成粒子旋轉環,粒子通過周圍的中子結合在一起。Wilkinson使用有效的角動量討論熱核物質的轉動,條件是可能遭受到中能重離子的碰撞,這種情況下可能會導致原子核環狀結構的出現,由緊挨著的α粒子和介於中間的中子對組成,如圖1.13(圖1.13 Wilkinson構想的環狀結團圖,大球代表α粒子,小球代表中子,α粒子被成對的中子束縛)。
圖1.11 三中心(a-c) 四中心(d-g) 分子軌道 圖1.12 ^{14}C的三角形結團結構 在豐中子碳同位素鏈中,能夠觀察到花朵狀結構。三個α例子的扁橢形變結構依然存在,加上
14 C的三角形形變和額外的中子,能夠得到較高階形變的扁橢密度,即花朵狀結團結構,如圖1.14,通過質子、中子和總的密度分布圖可知中子和質子具有不同的形變。
圖1.13 Wilkinson構想的環狀結團圖 1.2 實驗研究進展 實驗上通過非彈性碰撞,碎裂反應和敲出反應得到結團結構的信息。最簡單的情形是
8 Be具有雙α結構。這種類似啞鈴的結構導致產生轉動帶,該轉動帶的轉動慣量(Θ)與2:1的軸對稱形變對應。由於α粒子的結合能很大(~28 MeV),
6 Li和
7 Li分別表現為
4 He+d 和
4 He+t結團結構。
12 C中7.65 MeV的霍伊爾態可能是最著名的結團態。Hoyle在解釋宇宙中碳的豐度時,預言這個態的存在,後來通過實驗在靠近理論預言的能量位置測到了該態。碳核素在恆星環境中通過3α過程進行合成,首先兩個α粒子聚變形成
8 Be,然後在衰變之前俘獲第三個α粒子。
12 C主要通過7.65 MeV的0
+ 態先衰變到4.43 MeV的2
+ 態,然後放射性衰變到基態。具有3
α 結團結構的這個態與
4 He+
8 Be的衰變閾值十分接近,並且對俘獲幾率影響很大。由於該態具有極大的半徑(體積),所以能夠保證α粒子的準自由特性。考慮到
4 He是自旋為零的玻色子,該態可以通過玻色-愛因斯坦凝聚進行理解。理論預言該態存在更重的核素中,例如
16 O,甚至是
40 Ca,需要實驗的進一步檢驗。20世紀60年,原子核物理的加速器取得巨大進步,人們發展了重離子束流,首先觀察到
24 Mg的
12 C+
12 C結團結構。
圖1.14 ^{19-22}C的密度分布 實驗中入射粒子的能量和反應截面不斷改變。共振態的寬度約為100 keV,表明形成
24 Mg中間系統的時間比原子核穿過的時間要長。這些共振態後來被理解為
12 C+
12 C結團態。20世紀60年代,人們對
12 C+
12 C共振態的本質特徵進行了大量的嘗試,通過直接過程或間接過程進行了測量。間接法的實驗例如
12 C(
16 O,
24 Mg[
12 C+
12 C])
4 He。這裡的
24 Mg在核反應中形成,然後衰變成為兩個
12 C核,本質上是
12 C+
12 C散射實驗的時間反轉。這個方法近似的優點在於能夠得到一系列的結團態,而不必花費大量時間去記錄束流的能量。使用這個方法能夠得到激發能譜的類型,如圖1.15所示(圖1.15 a)
12 C(
16 O,
24 Mg
* )碎裂反應中觀察到的共振態-來自兩個不同的實驗,對應的
16 O束流能量分別為115 MeV和 160 MeV;b) 碎裂共振的能量-自旋對稱性。這個結團態位於具有低自旋的20 MeV激發能位置。較小的符號和實線表明
24 Mg低激發態的趨勢。)。激發能譜的峰值對應
24 Mg的共振態,在20到60MeV的激發能範圍內可以觀察到。
24 Mg的共振態衰變到
12 C+
12 C末態需要一個大的結團空間。使用實驗技術通過測量衰變產物的釋放角度,能夠推導出
24 Mg激發態的自旋和角動量
J ,如圖1.15b,水平軸為
J (
J+1 )。自旋為零時,
12 C+
12 C碎裂態位於線性中心,投影到激發能約為20MeV的位置。斜率的梯度明顯小於
24 Mg的基態。對於轉動結構,該激發態的能量為
E= (
h2 / 8π
2 Θ)J(J+1)。因此,通過實驗數據能夠提煉出對應的轉動慣量。圖1.16表明兩個
12 C核相互作用形成
24 Mg激發態的可能分布,對應的轉動慣量與實驗結構一致(圖1.16
24 Mg的
12 C+
12 C結團結構。這個圖像表明α粒子為兩個互鎖的三角形分布。每一個三角形與
12 C原子核有關。)。實際上,
12 C基態的對稱性和扁橢形變表明三個
α 粒子的三角形分布存在重疊。因此,
24 Mg的激發態也可能占據六個α粒子組態。類似地,更大尺度的結團結構被認為是
28 Si(
12 C+
16 O) 和
32 S(
16 O+
16 O),這一點與Ikeda、諧振子的預言一致。除了前面的例子,Ikeda圖(圖1.5)預言的結團結構還有很多在實驗中被觀察到。然而,對實驗的挑戰在於,在比
12 C更重的核中找到
Nα 結團結構的證據,例如
16 O 和
20 Ne等。這些核素中的結團結構有一些經典的例子,
20 Ne的基態就是一個很好的例子。
20 Ne的性質受α+
16 O結團結構的影響巨大,這主要是因為大量的反對稱性。因此,通過任何一個單獨的正宇稱態或負宇稱態不足以描述。相反地,正負宇稱態的線性組合是必須的。這個轉動態與兩個轉動帶有關,其中一個為正宇稱,另一個為負宇稱。兩個轉動帶的能量劈裂理解為
16 O核心兩邊的α粒子發生隧道效應的幾率。這與NH
3 中的氨分子占據反對稱結構類似。
圖1.15 圖1.16 ^{24}Mg的12C+12C結團結構 1.3 理論研究進展 大量的理論模型對原子核的結團進行了研究,包括微觀結團模型(共振群方法(RGM),生成坐標方法(GCM),正交條件方法(OCM),隨機變分方法(SVM),分子軌道(MO)模型,反對稱分子動力學(AMD)模型),費米分子動力學(FMD)模型,有效液滴模型(ELDM),密度依賴的結團模型(DDCM)和協變密度泛函理論。
1.3.1 微觀結團模型概述 20世紀60年代的早期,隨著共振群方法(RGM)的出現,微觀結團模型得到了顯著的發展。接下來的二十年里,結團物理的發展受RGM的影響很大,同時出現了一些新的模型,例如生成坐標方法(GCM) 和正交條件方法(OCM) ,可以用於輕的p殼核的研究。這三種方法成為描述結團間相對運動的傳統微觀模型。方法中最重要的是對結團間泡利原理的處理和結團間相對運動的細節描述。在處理泡利阻塞效應的時候,RGM 和GCM全是微觀的,OCM是半微觀的。RGM明確給出結團間相對運動波函式的動力學坐標,因為要分開具有反對稱性的內部坐標和相對坐標很難,所以少體結團系統在實際套用中有一些限制。
為了將GCM方法用於結團模型研究,Brink採用多中心結團基的波函式,也稱Bloch–Brink波函式。Bloch–Brink波函式被寫成斯萊特行列式,同時通過結團中心的幾何位置進行參數化表示。GCM計算通過Bloch–Brink波函式的疊加進行,對結團中心的位置採用相對距離參數作為生成坐標。原則上,基於Bloch–Brink整個模型空間的GCM方法與RGM等價。微觀地講,使用GCM方法能夠用於重核系統和多結團系統的計算。除了兩體系統之外的多體系統,Bloch–Brink波函式的模型空間有時被縮短。具有縮短模型空間的GCM方法在描述強耦合圖像的態(重疊本徵態的觀點)非常有用,這個態描可通過Hartree–Fock框架下的GCM進行描述。另外,RGM與弱耦合圖像(基於具有好的宇稱和角動量)直接相關。
自從20世紀60年代,由於波函式的有效性,Bloch–Brink α 結團模型被廣泛用於α結合系統(Z = N 核素)。基於Bloch–Brink α 結團模型,為了研究sd 殼核的激發態,模型空間通常使用一個簡單的Bloch–Brink波函式進行縮小,同時進行了一些擴展運算,例如不加約束的三軸計算。另外,推轉方法也進行了套用,也進行過投影的變分計算。
人們對不穩定核感興趣,結團方法被擴展和套用於研究不穩定核的結團結構。其中之一是研究核心周圍的價核子性質。為了研究中子暈核,例如6 He和11 Li,通過多個群對核心、價中子進行三體計算取得了巨大的成功。Baye和Descouvemont使用具有兩個α粒子和價中子Bloch–Brink波函式的GCM方法研究Be同位素的結團結構。使用隨機變分方法(SVM)對不穩定p殼核的多結團系統進行了精確計算。
分子軌道(MO)的結團模型成功描述了豐中子Be同位素鏈的結團結構。分子軌道模型基於平均場中獨立的單粒子軌道圖像,該平均場由多中心結團結構形成,Be同位素鏈的結團結構被描述成由兩個α粒子核心和價中子組成。使用包含核子-核子相互作用和反對稱性的分子軌道模型對Be和C同位素鏈進行微觀計算。後來,Itagaki使用擴展的分子軌道圖像來處理價核子與結團間相對運動的關係。
AMD模型不依賴於結團核心存在的假設。儘管本徵態的模型空間基於斯萊特行列式或幾個斯萊特行列式的線性組合,它最大的優點是適用於很大範圍內一般核。AMD模型被廣泛用於描述遠離N =Z 線條的核素,這些計算表明豐中子核中的α粒子十分明顯。
對比精確描述核子相互作用的多核子系統,前面的結團計算被當做模型,通常採用有效的核力,同時將模型空間縮短。這裡我們必須指出,最近在使用採用實際核力的量子蒙特卡羅方法對超越少體系統的多體系統(A
)的描述中取得了巨大的進步。計算中同樣發現
8 Be具有雙α結團結構。因為精確的多體計算需要進行大量的數值計算,關於激發態的計算仍然僅限於輕核(
)。
1.3.2 費米分子動力學模型 為了描述原子核的基態以及低於產生粒子能量區域的重離子反應,H. Feldmeier在1990年提出了費米分子動力學模型(FMD)。FMD的多體試驗態是由單粒子高斯波包|
ql (t)>的斯萊特行列式|
Q (t)>,其中
ql (t)代表一系列的單粒子參數
ql (t)={
,a
l (t),χ
l (t),ξ
l (t)},
=r
l (t)+ia
l (t)
包含了平均位置,平均動量和複雜的寬度。自旋自由度通過自旋量|χ
l (t)>表示,
同位旋部分具有時間依賴,能夠識別任何一個質子或中子。所有參數的運動方程通過變分原理得到。哈密頓量是有效的,因為核子間的相互作用造成了強烈的短程排斥引起關聯,這種關聯不能通過試驗態|Q (t)>進行描述。而且強烈的張量力引起的自旋關聯性,只通過單一的斯萊特行列式表達是不充分的。
FMD模型的基態即能量H(Q
* ,Q)=<Q|
H |Q>取極小值的點。因為所有的廣義力
在極小點不存在,該態是靜止的,所有
。
,
等參數中不存在費米運動,基態性質例如結合能和均方根半徑能夠通過一系列的核子-核子相互作用再現。這些有效的核子-核子相互作用對動量依賴不同,但是原子核的本徵結構依賴於相互作用。為了更加精確描述原子核的結構,需要考慮單粒子態和斯萊特行列式的重疊,例如暈核。FMD能夠模擬從熔合到耗散、多重碎裂的一系列重離子反應。和含時Hartree-Fock方法不同,這些結果包含了由基態本徵結構得到的初始關聯,該關聯在模擬碎裂反應時扮演重要角色。
對時間依賴的寬度參數是一個重要的非經典的自由度,特別允許核子蒸發,要不就強烈阻礙,因為每次溢出的波包至少會帶走零點能。原子核內部的這個零點能典型值為10 MeV,但是被蒸發的核子僅2 MeV的動能。因此,波包在蒸發的過程中必須傳播。使用FMD對時間求平均可以確定熱動力學平衡性質。受限制參數設定可能會導致不存在精確解,同時波包的分裂是量子分支的重要來源,該動力學自由度的缺乏會對結團的形成造成強烈阻礙。
1.3.3 有效液滴模型 為了更好地描述α衰變和結團放射性,M. Gonqalves等提出了有效液滴模型。該模型已用於研究冷裂變反應,同時討論不同的慣性參數對半衰期和產物的質量產額分布的影響。因為該模型限制最小的碎片釋放,因此,該模型能夠用於研究質子釋放現象。依據有效液滴模型,球形的分子是存在的,為了得到庫侖勢能和表面勢能的解析表達式需要計算總勢壘。伽莫夫滲透因子通過兩個係數進行計算:Werner-Wheeler慣性係數和有效慣性係數。
在分子相過程中,形變系統的幾何構造為兩個不同半徑的交叉幾何球體。為了完整地描述這種結構,我們需要四個獨立的坐標,而忽略質心的位置。圖1.17是典型的雙核衰變系統結構圖,選擇特定的坐標:每個球面弓形的半徑為
R 1 和
R 2 ;最大的球面弓形頂點為ξ;兩個幾何中心間距為ζ。在分子相的末期,整個系統會使兩個球形的相切碎片解體,對應的碎片和子核的半徑分別為
和
。
圖1.17 雙核衰變系統的結構圖 1.3.4 密度依賴的結團模型 圖1.18 中心核和α粒子的矢量圖 密度依賴的結團模型能夠用於描述α 衰變和結團放射性。半衰期通過薛丁格方程的準束縛解得到,許多核的理論結果和實驗結果符合得很好,包括N =126殼周圍的奇特α釋放,α衰變同核異能態和超重核。對於核心和α粒子組成的系統,可以簡化成為無結構的α結團圍繞核心做軌道運動,它們之間相互作用的勢能包括庫侖排斥勢,核力吸引勢以及離心勢,表達式為:
其中,
μ 是α核心繫統的折合質量,
是α結團的角動量。使用雙摺疊模型去構建庫侖勢和核力勢。核力勢通過密西根三程湯川秀樹-里德類的有效核子-核子相互作用得到,包括密度和能量依賴項。庫侖勢仍然使用雙摺疊模型,只是將原子核的密度分布改成電荷密度分布。勢場的密度具體如下:
λ (1.3)
其中λ用於重整化核勢去再現等價的局域勢(λ=1是庫侖勢),
s 是α粒子和核心原子核的相對距離,
是有效的核子-核子相互作用,
和
分別是α粒子和核心原子核的密度分布。雙摺疊的坐標矢量如圖1.18所示(圖1.18 中心核和α粒子系統在雙摺疊模型中的坐標矢量示意圖)。
α 結團的球形密度分布採用高斯分布的形式:
中心核子的密度分布來自於實驗上已知的電荷分布,16 O,40 Ca, 90 Zr和208 Pb的中心核密度分別為:
α粒子相對於中心核的相對運動,可以用靜態薛丁格方程表達,形式為 :
精確求解上述方程可以得到α結團的信息。
1.3.5 協變密度泛函理論 關於核結構的研究使用最廣泛的方法是協變密度泛函理論。原子核能量密度泛函理論的實質類似於Kohn-Sham密度泛函理論,後者廣泛用於凝聚態物理和量子化學中的電子結構計算。在原子核物理中,多體動力學表現為獨立的核子在局部自洽的平均勢場中運動,可以得出相應的密度和流。
相對論和非相對論的能量密度泛函理論用於描述核物質和有限核,給定核子相互作用的原子核能量密度泛函理論具有普適性,對於所有的系統具有相同的形式。通過使用同類核物質的實驗性質和有限核的實驗數據,只需要調節少量的參數,一個普遍的泛函形式就可用於描述所有的核子,因此可以描述輕核的結團性質。
P.Arumugam等使用無對關聯的相對論平均場理論對輕核區的部分核素進行研究,得到了基態和激發態的多種結團結構。法國的J. P. Ebran等使用能量密度泛函的框架,對原子核的結團和量子液滴進行了研究,結果表明勢阱的深度決定了兩個單粒子軌道之間的能量空隙,從而使波函式局域化,相應的核子結團的密度分布更加狹窄,結團結構更加明顯。張煒等人使用絕熱近似和非絕熱近似下的相對論平均場理論,研究
24 Mg的勢能曲面,同時分析密度分布得到可能的環狀態,結果表明
24 Mg的環狀態多傾向於極端扁橢情形
,並且取最小環狀的激發能為
,四極形變為
。耿立升等使用反射不對稱的相對論平均場理論對
226 Ra的八極形變的結團結構進行研究,與實驗結果吻合得很好。我們組使用介子交換和點耦合的協變密度泛函理論對Be的同位素鏈的結團結構進行了研究,表明
8,10,14 Be具有明顯的雙α結團結構。
 圖1.1 ^{16}O的4α結團結構
圖1.1 ^{16}O的4α結團結構 圖1.2 中子滴線核易形成結團
圖1.2 中子滴線核易形成結團 圖1.3 輕元素的單核子結合能
圖1.3 輕元素的單核子結合能 圖1.4 (上) 結合能,(下) α粒子分布。
圖1.4 (上) 結合能,(下) α粒子分布。 圖1.5 Ikeda圖
圖1.5 Ikeda圖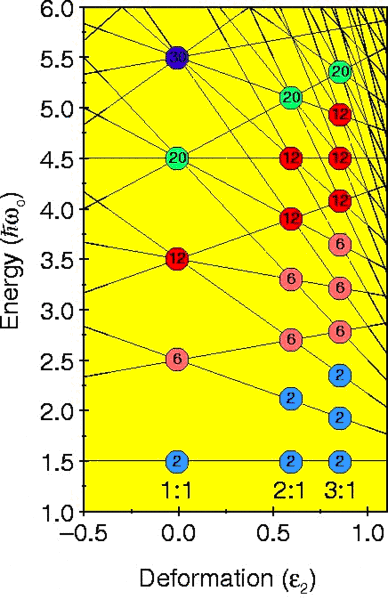 圖1.6 形變諧振子的能級
圖1.6 形變諧振子的能級 圖1.7 2:1 、3:1, 4:1形變軸的密度分布圖
圖1.7 2:1 、3:1, 4:1形變軸的密度分布圖 圖1.8 Be同位素鏈的分子軌道的形成
圖1.8 Be同位素鏈的分子軌道的形成 圖1.9 ^{8}Be和^{9}Be的轉動帶
圖1.9 ^{8}Be和^{9}Be的轉動帶 圖1.10 改進的Ikeda圖
圖1.10 改進的Ikeda圖
 圖1.11 三中心(a-c) 四中心(d-g) 分子軌道
圖1.11 三中心(a-c) 四中心(d-g) 分子軌道 圖1.12 ^{14}C的三角形結團結構
圖1.12 ^{14}C的三角形結團結構 圖1.13 Wilkinson構想的環狀結團圖
圖1.13 Wilkinson構想的環狀結團圖 圖1.14 ^{19-22}C的密度分布
圖1.14 ^{19-22}C的密度分布 圖1.15
圖1.15 圖1.16 ^{24}Mg的12C+12C結團結構
圖1.16 ^{24}Mg的12C+12C結團結構












 圖1.17 雙核衰變系統的結構圖
圖1.17 雙核衰變系統的結構圖 圖1.18 中心核和α粒子的矢量圖
圖1.18 中心核和α粒子的矢量圖














