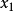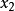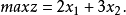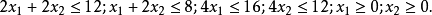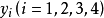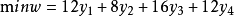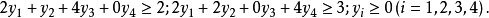原問題

原問題，又稱原線性規劃問題，是指每一個線性規劃的原始問題，每個原問題均可以轉化為與其對稱的對偶問題。

基本介紹

• 中文名：原問題
• 外文名：Primal problem
• 拼音：Yuán wèn tí
• 學科：運籌學
• 別稱：原線性規劃問題
• 對稱：對偶問題

內容概述

最最佳化理論研究的是在眾多的方案中哪種方案最優，以及怎樣找出最優方案的問題。該理論發展至今已出現線性規劃、整數規劃、非線性規劃、幾何規劃、動態規劃、隨機規劃、網路流等眾多分支，其中線性規劃與非線性規劃是最最佳化理論的重要分支，也是最基本的部分。線性規劃中普遍存在配對現象，對每個線性規劃問題，都有另一個與其密切相關的線性規劃問題存在，其中前者稱為原問題，而後者即為它的對偶問題。

轉化規則

原問題與對偶問題是相對的，二者為同類型的規劃，構成對偶規劃的一般規則如下：

1. 若原問題是極大化問題，那么對偶問題就是極小化問題；若原問題是極小化問題，那么對偶問題就是極大化問題。
   
2. 在原問題與對偶問題中，約束右端向量與目標函式中係數恰好對換。
   
3. 對於極小化問題的“≥ ”型約束(極大化問題的“≤ ”型約束)，相應的對偶變數有非負限制；對於極小化問的“≤ ”型約束(極大化問題的“≥ ”型約束)，相應的對偶變數有非正限制；對於原問題的“=”型約束，相應的對偶變數無正負限制。
   
4. 對於極小化問題的具有非負限制的變數(極大化問題的具有非正限制的變數)，在其對偶中相應的約束為“≤ ”型不等式；對於極小化問題的具有非正限制的變數(極大化問題的具有非負限制的變數)，在其對偶問題中相應的約束為“≥ ”型不等式；對於原問題中無正負限制的變數，在其對偶問題中相應的約束為等式。
   

舉例

原問題：某企業計畫生產甲、乙兩種產品，該兩種產品均需要A、B、C、D 四種不同的材料，按工藝資料規定，生產一單位甲乙產品需要各種材料數量及單位產品利潤如表中所示。問：如何安排產品的生產計畫，才能使企業獲利最大?

產品設備	A	B	C	D	單位利潤
甲產品	2	1	4	0	2
乙產品	2	2	0	4	3
現有材料數量	12	8	16	12

解：設企業生產甲產品為 件，乙產品為 件，則

目標函式：

約束條件：

對偶問題：如果另外一企業想將上述企業擁有的資源收買過來，至少應付出多少代價，才能使第一個企業願意放棄生產活動，出售資源？

解：設第i種資源單位增值價（售價=成本+增值）為 ，則

目標函式：

約束條件：

套用

線性規劃的原問題與對偶問題的對應關係決定了二者之間可通過一定規則相互轉化。因此可將複雜的原問題轉化成其對偶問題進行解決，從而簡化線性規劃問題。教師在教學中可以引導學生將運籌學知識點進行歸納總結，以加深理解，提高學習效率的觀點。並以線性規劃中原問題與對偶問題轉化為例，探討了轉化規律的總結過程及其教學體會，為運籌學教學中對其它知識點的歸納總結提供了啟示。