卡麥可數

卡麥可數的定義是對於合數n，如果對於所有與n互質的正整數b，都有同餘式b^(n-1)≡ 1 (mod n)成立，則稱合數n為Carmichael數。

2016年物流工人余建春帶著自己的五項數學發現登上了浙江大學數學系的講台，與教授和博士生們“同堂論道”，最具價值的發現是一組“卡麥可數”（Carmichael數）的判別準則。

基本介紹

• 中文名：卡米切爾數
• 外文名：Carmichael
• 別名：Carmichael數
• 表達式：每個Carmichael至少是三個不同素數的乘積
• 例子：561=3*11*17

定理介紹

1. 每個Carmichael至少是三個不同素數的乘積。如561=3*11*17。

費馬小定理(Fermat theorem)：

設p為一素數，對於任意整數a，有a≡ 1 (mod p)。

假如p是質數，且gcd(a,p)=1，那么 a^(p-1) ≡1（mod p） 假如p是質數，且a,p互質，那么 a的(p-1)次方除以p的餘數恆等於1

性質

卡麥可數有至少3個正素因數。如圖一是首個k個正素因數的卡麥可數，k=3,4,5,...：

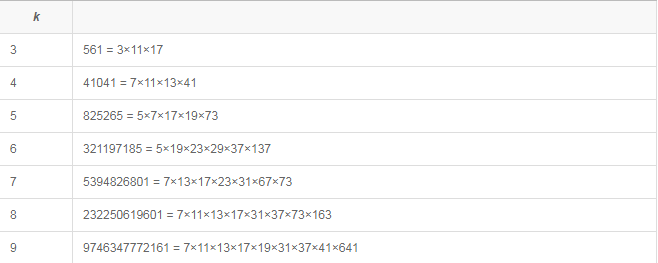
圖一

如圖二是首十個有4個素因數的卡麥可數：

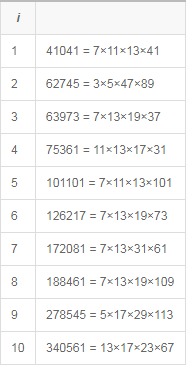
圖二

費馬判定

設p為一素數，而a與p互素，則 a^p - a 必為p的倍數。 利用費馬小定理，對於給定的整數n，可以設計一個素數判定算法。通過計算d=a^(n-1)mod n來判定整數n的素性。當d不等於1時，n肯定不是素數；當d等於1時，n則很可能是素數。但也存在合數n使得d=a^(n-1)≡1(mod n)。例如，當a=2時，滿足d=1的最小合數是n=341。為了提高測試的準確性，我們可以隨機地選取多個a對a^(n-1)mod n的結果進行測試。能通過全部a的測試的合數n，被稱為Carmichael數，前3個Carmichael數是561,1105,1729。Carmichael數是非常少的。在1~100000000範圍內的整數中，只有255個Carmichael數。

素性檢驗

由費馬小定理可得，若n為素數，則對任意整數b，且b和n互素，都有b(mod n) ≡1。因此，若存在整數b，使得b(mod n)≡1不成立，則n是一個合數。

利用上述結論，對於給定的整數n，可以設計一個素數判定算法。

1.隨機選取整數b，2<=b<=n-2，計算d =b(mod n)。當d不等於1時，n是合數；當d等於1時，n則很可能是素數，對於本次判斷來說，判斷錯誤的機率為1/2。

2.如此重複多次，可以將判斷錯誤的機率降低至期望值以下。

但是，上述方法有缺陷。因為Carmichael數的存在，可導致上述算法給出一個錯誤的判斷。

前3個Carmichael數是561,1105,1729。Carmichael數是非常少的。在1~100000000範圍內的整數中，只有255個Carmichael數。

列舉數組

列舉100000000以內的255個卡米切爾數，括弧內為它的最小因子：

561(3)

1105(5)

1729(7)

2465(5)

2821(7)

6601(7)

8911(7)

10585(5)

15841(7)

29341(13)

41041(7)

46657(13)

52633(7)

62745(3)

63973(7)

75361(11)

101101(7)

115921(13)

126217(7)

162401(17)

172081(7)

188461(7)

252601(41)

判別準則

2016年物流工人余建春帶著自己的五項數學發現登上了浙江大學數學系的講台，與教授和博士生們“同堂論道”，最具價值的發現是一組“卡麥可數”（Carmichael數）的判別準則。

“卡麥可數”是一種偽素數（偽質數），在一億以內的正整數中只有255個。蔡天新驗證了余建春提出的公式，認為在一定範圍內，余建春的發現能夠以更高的效率找出更多的“卡麥可數”。

他的新算法同時得到了國際學術界的普遍讚賞。密蘇里大學數學家William Banks告訴CNN ，這種算法一經確認，即可成為卡麥可數領域的一大重要發現。