基本介紹
- 中文名：卡方檢驗量
- 外文名：Chi-SquareStatistic
- 分類：計算機 統計
- 提出：pearson
- 適用於：卡方檢驗
- 提出時間 ：1900年
定義,功能,公式,特點,卡方檢驗,
定義
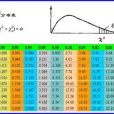
卡方統計量是指數據的分布與所選擇的預期或假設分布之間的差異的度量。在1900年由英國統計學家pearson提出，是用於卡方檢驗中的一個統計量。
功能
它可用於檢驗類別變數之間的獨立性或確定關聯性。例如，如果有一個按投票者性別分類的選舉結果的雙因子表，卡方統計量可幫助確定投票是否獨立於投票者的性別，或者在投票與性別之間是否存在關聯。如果與卡方統計量相關聯的p值小於選定的a水平，檢驗將拒絕兩個變數彼此獨立的原假設。
也可用於確定某個統計模型是否能夠充分擬合數據。例如，Logistic回歸將計算卡方統計量以評估模型的擬合情況。如果與卡方統計量相關聯的p值小於選定的a水平，檢驗將拒絕模型與數據相擬合的原假設。另一個示例是“基本統計量”選單中的用於Poisson數據的擬合優度檢驗，它使用卡方統計量來確定數據是否服從Poisson分布。如果數據為離散數據，則可以報告每個類別對卡方值的貢獻，從而量化每個類別差異對總卡方值有多大影響。例如，如果一個擬合優度檢驗拒絕了原假設，則這個結果是因為所有類別與預期稍有差異還是因為有一個類別與其預期極大不同導致的？假設您預期一盒蠟筆中包含一根藍色、一根紅色以及一根綠色的蠟筆，但實際上它包含一根藍色和兩根綠色的蠟筆，而沒有紅色的蠟筆。“綠色”和“紅色”類別與預期不符，但“藍色”相符。因此，“藍色”並不影響所生成的卡方值；數據中的所有差異均來自“綠色”和“紅色”類別。
公式
卡方統計量是由統計學家皮爾遜於1900年提出的用於檢驗實際分布與理論分布配合程度，即配合度檢驗的統計量。它是由各項實際觀測次數（
）與理論分布次數（
）之差的平方除以理論次數，然後再求和而得出的，其計算公式為：
理論次數越大，該分布與卡方分布越接近，當理論次數
時，與卡方分布符合較好。當超過20%的理論次數小於5，或至少有一個理論次數小於1時，公式右邊的表達式與卡方分布偏離較大。因此，其套用條件為至少有80%的理論次數不小於5，並且每個理論次數都不小於1。
特點
理論次數不符合要求時採用卡方檢驗
在實際套用中，卡方檢驗公式的適用條件為：80%以上的理論次數大於5，並且所有的理論次數不能小於1。在實際研究中，當單元格的理論數據過小時，一般採用下列幾種方法進行處理：
（1）增加樣本容量。如果在數據處理之前發現問題，並且補充被試可以保證測試條件不變，對研究結果沒有影響，則可以補加被試，使數據符合檢驗要求。
（2）合併單元格。在一個分類指標為順序變數時，如果出現理論次數過小的情況，可以調整分類項，將單元格加以合併。如學生成績分為優、良、中、差，如果成績為差的學生極少，使得卡方檢驗的條件不符合，則可以把“差”與“中”合併為“中及其以下”。
（3）取消部分單元格。當分類指標為稱名變數時，若出現理論次數過小的情況，如果採用合併單元格的方法，應該合併到哪個類別及合併後類別的實際意義將不明確，這時應縮小研究範圍，去除這些類別。
（4）使用連續校正（correction for continuity）公式。若四格表的理論次數大於5但小於10，這時可以根據四格表屬於相關四格表還是獨立四格表，採用相應的連續性校正公式計算卡方值。
（5）費舍精確機率（Fisher’s exact probability）檢驗法。當總數不大於20時，如果出現理論次數小於5的情況，可計算費舍精確機率進行檢驗。
卡方檢驗
卡方檢驗就是統計樣本的實際觀測值與理論推斷值之間的偏離程度，實際觀測值與理論推斷值之間的偏離程度就決定卡方值的大小，卡方值越大，越不符合；卡方值越小，偏差越小，越趨於符合，若兩個值完全相等時，卡方值就為0，表明理論值完全符合。
注意：卡方檢驗針對分類變數。
1、提出原假設：
如果總體分布為離散型，則假設具體為：
2、將總體X的取值範圍分成k個互不相交的小區間
，如可取
其中
可取
，
可取
，區間的劃分視具體情況而定，但要使每個小區間所含的樣本值個數不小於5，而區間個數k不要太大也不要太小。
3、把落入第i個小區間的Ai的樣本值的個數記作fi，成為組頻數（真實值），所有組頻數之和
等於樣本容量n。
4、當為真時，根據所假設的總體理論分布，可算出總體X的值落入第i 個小區間
的機率
，於是，
就是落入第i個小區間Ai的樣本值的理論頻數（理論值）。
5、當為真時，n次試驗中樣本值落入第i 個小區間Ai的頻率與機率應很接近，當不真時，則相差很大。檢驗卡方統計量，在假設成立的情況下服從自由度為k-1的卡方分布。
