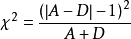四格表

人為劃分的四格表使用皮爾遜餘弦相關

真正的獨立二分變數使用phi相關或卡方檢驗或者Z檢驗

相關二分變數使用Mc方法

基本介紹

• 中文名：四格表
• 外文名：Four form
• 基本思想：假設檢驗

皮爾遜餘弦相關

如果兩個變數都是連續性變數且服從常態分配，人為劃分為兩個類別，則不能用phi相關。

以下是一種近似算法：

舉例：歷史成績是否及格是人為二分，地理成績是否及格也是人為二分，a代表歷史地理都及格，d代表歷史地理都不及格。

注意：性別、是否得某種疾病是真正二分，不能用這種算法

獨立二分樣本檢驗

n=a+b+c+d	癌症	其他
吸菸	a	b
非吸菸	c	d

如果兩個變數是真正二分的不連續變數，且二者獨立

法1： 檢驗

法2：卡方檢驗 先計算邊際機率，再給出理論數，最後進行計算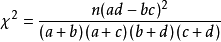

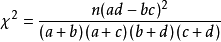
法3：比率差異檢驗（Z檢驗）

聯繫：

檢驗和卡方檢驗 。 係數的優點在於小於1， 係數大於0.6表示強的相關，小於0.3表示弱的相關。卡方的優點在於有對應的機率可以查找。

Z檢驗的統計量平方就是卡方檢驗

注意：卡方檢驗的自由度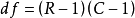，對四格表而言R=C=2，

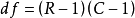
矯正公式

四格表有一格理論次數小於5，需要用矯正公式

相關樣本檢驗

	第一次同意	第一次反對
第二次反對	A	B
第二次同意	C	D

由McNemar提出，如果兩個變數相關（例如同一批人對同一個問題表明意見）

矯正公式

四格表有一格理論次數小於5，需要用矯正公式