卡帕曲線

卡帕曲線是一種由圓產生的曲線，半徑為定長a的動圓C的圓心在二軸上滑動。

基本介紹

• 中文名：卡帕曲線
• 外文名：Kappa curve
• 別稱：Gutschoven曲線
• 學科：數學

簡介

卡帕曲線(Kappa curve)從坐標原點O向圓C所作切線的切點M的軌跡稱為卡帕(K)曲線(見圖).它的極坐標方程為p=a cot B，直角坐標方程為y2(x2-f-yz)= a2x2. 17世紀斯呂塞(Sluse，R. -F. de)與惠更斯(Huygens , C.)在通信中第一次提到卡帕曲線.當時是為了解答下面的運動學問題:同一平面內有一個固定的直角坐標系二勿和一個運動的直角坐標系x' Or y'，已知xr軸始終通過點o, y'軸與x軸的交點C到。‘的距離等於定長a，求動坐標系的原點。‘的軌跡.這裡的點}r相當於圖中的點M，rM,x軸相當於直線MO。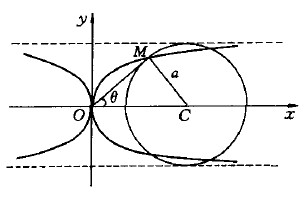

有關研究歷史

卡帕曲線（kappa curve）也稱為Gutschoven曲線（Gutschoven's curve），是外形類似希臘字母ϰ的二維代數曲線。

Gérard van Gutschoven在1662年就開始研究此一曲線。

Kappa曲線是伊薩克·巴羅第一批用rudimentary calculus來判斷曲線切線的曲線之一。

艾薩克·牛頓及約翰·白努利後來也有研究過此曲線。

方程表示

Kappa曲線在笛卡兒坐標系下的方程為

其參數方程為

極坐標系的方程簡單很多

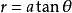
Kappa曲線有二條垂直的漸近線，為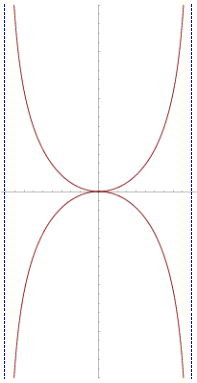

Kappa曲線有二條垂直的漸近線

在右圖中以虛線表示。

Kappa曲線的曲率：

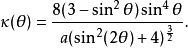
切線角為：