基本介紹
- 中文名:南部力學
- 外文名:Nambu Mechanics
- 領域:經典力學
介紹
單自由度情形
哈密頓力學





南部力學




多自由度情形
與剛體力學的聯繫

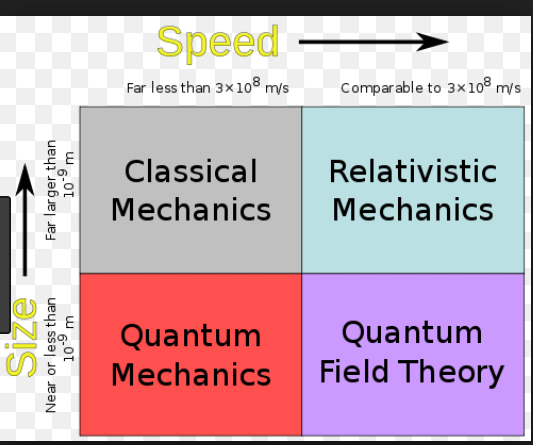










經典力學自牛頓創立以來,經拉格朗日和哈密頓等人的努力發展成為分析力學,並向剛體力學、彈性力學、流體力學等具體領域繼續推進。1973年,南部陽一郎提出一種邏輯上自洽的廣義力學體系,稱為南部力學。介紹經典力學自牛頓創立以來,...
第一章 牛頓力學 第二章 運動學 第三章 拉格朗日力學變分原理的微分形式 第四章 拉格朗日力學變分原理的積分形式 第五章 力學的正則形式哈密頓力學 第六章 剛體動力學轉動 第七章 振動與波彈性力學 第八章 流體力學 第九章 相對論力學 第十章 廣義相對論力學 附錄一 矩陣及其本徵值問題 附錄二 南部力學 ...
地質力學在中國是由李四光創立的。最初是從1921年研究中國北部石炭紀、二疊紀含煤地層開始。1924年以後,李四光對比了中國南部和北部石炭–二疊紀及地球上其他地區同一時期,特別是古生代以後海進、海退現象,認為大陸上海水的進退,不僅是海面的升降,可能還有由赤道向兩極,反過來由兩極向赤道的方向性的運動。據此,他...
南部陽一郎 (日語平假名:なんぶ よういちろう,英語:Yoichiro Nambu,1921年1月18日-2015年7月5日),美籍日裔理論物理學家,出生在日本福井縣,後加入美國國籍,博士學位,畢業於東京大學。也是大阪市立大學特別榮譽教授,芝加哥大學名譽退休教授,2008年諾貝爾物理學獎獲得者之一。從20世紀60年代起,他就在...
《經典力學》是2023年科學出版社出版的圖書。內容簡介 《經典力學》是以分析力學為主要內容的經典力學入門教材, 是作者在中山大學講授“理論力學”課程自編講義的基礎上, 進一步梳理、凝練而成的.《經典力學》共分17 章. 其中第1~7 章為拉格朗日力學, 包括變分法、位形空間、相對論時空觀、最小作用量原理、對稱...
南部-戈德斯通定理(Nambu-Goldstone Theorem)指連續對稱性被自發破缺後必存在零質量玻色粒子這一定論,此粒子被稱為戈德斯通玻色子(或稱南部-戈德斯通玻色子)。這個定理在粒子物理中有著重要套用,如π介子就是對應著近似手征對稱性破缺的戈德斯通玻色子。粒子物理學 粒子物理學是研究組成物質和射線的基本粒子以及它們...
如果不僅簡單的利用辛流形上的光滑函式的結合代數,哈密爾頓系統可以用更一般的交換有單位的實泊松代數表述。一個狀態是一個(裝備了恰當的拓撲結構的)泊松代數上的連續線性泛函,使得對於代數中的每個元素A,A映射到非負實數。進一步的推廣由南部力學給出。相關條目 ADM形式 廣義相對論中的質量 ...
趙子福,男,1973年1月出生於四川省南部縣,博士,中國科學技術大學教授、博士生導師。人物經歷 1996年獲中國科學技術大學理學學士學位(地球化學),2001年獲中國科學技術大學理學博士學位(地球化學)。2001年8月至今在中國科學技術大學從事教學和科研工作,2004年1月被聘為副教授,2008年1月被聘為教授。獲2004年國家...
汪林兵教授現任或曾經擔任以下職務:維吉尼亞理工大學終身教授,可持續性交通基礎設施研究中心副主任; 美國土木工程協會(ASCE)工程力學研究所路面力學工作委員會第一任主席(創始人);北美華人交通協會路面委員會主席;聯邦公路局瀝青混凝土基本特性和高級模擬專家委員會委員;ASCE非彈性行為委員會委員;ASCE瀝青材料委員會委員...
何曉英,女,1955年出生,四川南部縣人,中國共產黨黨員,西華師範大學優秀碩士導師,西華師範大學電化學研究所副所長。人物經歷 1982年1月畢業於南充師範學院(現西華師範大學)化學系,獲學士學位。同年留校任教,曾任化學系副主任,現為化學化工學院黨總支委員、教工黨支部書記, 西華師範大學電化學研究所副所長,...
郭令智(1915年4月4日—2015年8月5日),中國科學院院士,地質學家,生於湖北安陸。曾任南京大學教授、副校長、代校長。1938年畢業於中央大學地質系。1993年當選為中國科學院院士。2015年8月5日於南京逝世。郭令智長期從事中國南部和東南部區域大地構造研究,在華南首次發現板塊運動和俯衝碰撞所形成的江南元古代溝弧...
戴思銳教授,1945年1月18日出生於四川省南部縣,1969年畢業於中國農業大學的前身北京農業大學農業經濟管理系,1982年在西北農業大學農經系獲碩士學位,1982年到西南大學經濟管理學院全職任教。1988年被評為農業部有突出貢獻專家,1991年享受政府特殊津貼,1993年評為博士生導師,1998年被評為國家有突出貢獻專家。兼任全國...
主要有《廣西富賀鐘區鈾礦之發現》、《對於湘南山系構造的幾點意見》、《湖南大義山系構造並略述中國南部走向北偏西十度至二十度之構造關係》、《中國顯著的經向構造帶及有關的磁力重力異常》、《長期重力下岩石的非彈性變形》、《地質力學簡介》等,發表了近百篇地質考察報告和科研論文。60年代,多次出國考察,...
近年來在青藏高原東南部區域開展了一系列的地震波接收函式、地殼內地震波各向異性和有限頻的層析成像研究,詳細探討了該地區的地殼增厚和地面隆升的動力學問題,尤其是地殼和岩石圈的構造及演化等過程。社會兼職 《Physics of the Earth and Planetary Interiors》國際重要期刊審稿專家 中國地球物理學會(CGS)會員 勘探...
3. 張雲, 薛禹群, 施小清等. 飽和砂性土非線性蠕變模型研究, 岩土力學, 2005, 26(12): 1869-1872. (EI)4. 姜蓓蕾, 吳吉春, 楊儀, 施小清. 張家港市合興地塊淺層地下水資源評價. 水利水電科技進展, 2005, 25(增刊): 8-11.5. 施小清, 薛禹群, 張雲等. 常州地區粉質粘土的蠕變模型. 工程勘察, 2006,...
1931年,第二屆國際科學技術史大會上,蘇聯代表團的黑森(Hessen)運用馬克思辯證唯物主義和歷史唯物主義的觀點來分析牛頓力學的發生與發展,做了題為“牛頓力學的社會經濟根源”的報告。蘇聯代表團的論文結集出版,取名為《走到十字路口的科學》,貝爾納為此書專門寫了書評,發表在右翼的《旁觀者》雜誌上。他思想所受到...
11. 史宇坤,楊湘寧,劉家潤。2012 。貴州南部宗地地區早石炭世- 早二疊世的䗴類。北京:科學出版社。271 頁。12. Yukun SHI ,Hao Huang , Xiaochi Jin , Xiangning Yang. 2011. Early Permian fusulinids from the Baoshan Block, western Yunnan, China. Journal of Paleontology. 85(3): 489-501.13....
(12)鄧賓, 劉樹根, 王國芝, 李智武, 劉順, 曹俊興. 四川盆地南部地區新生代隆升剝露研究-低溫熱年代學證據. 地球物理學報. 2013, 56(6): 1958-1973.(13)Bin Deng, Shugen Liu, Sun Liu, Luba Jansa, Zhiwu Li, Yong Zhong. Indosinian Progressive N-S Deformation of the Jiaochang structure in ...
張翀,吳世敏,丘學林. 南海南部海區前陸盆地形成與演化. 海洋地質與第四紀地質,2007,27(1):61-70 趙明輝,丘學林,徐輝龍,施小斌,吳世敏,葉春明,夏少紅. 南海北部沉積層和地殼內低速層的分布與識別. 2007,自然科學進展,17(4):471-479 吳世敏,楊 恬,周 蒂,丘學林,夏斌,南海南北共軛邊緣伸展模型...
船底座星雲(Carina Nebula):船底座星雲是天空中最大、最明亮的星雲之一,位於船底座南部,距離地球約7600光年。星座神話 傳說希臘英雄伊阿宋率領眾勇士乘從“阿爾戈”號大船去覓取金羊毛,經過許多磨難,最後終於取得金羊毛,凱旋而歸。後來,女神雅典娜把這艘海船提到天上成為南船座。但由於南船座範圍太大,1750年...
8塔里木盆地南部的鐵克里克推覆體與中新生代前陸盆地的構造與油氣領域 8.1鐵克里克逆沖推覆構造及山前逆沖斷層帶 8.2塔里木盆地南部的中新生代前陸盆地的結構與構造 8.3塔里木盆地南部中新生代前陸盆地油氣勘探領域 9結論與問題 9.1在古生代塔里木板塊及其大陸邊緣盆地的原型及其形成、演化地球動 力學方面 92關於...
54 張協奎,張亞芬.南部沿海主要港口空間結構分析及互聯互通定位.廣西民族大學學報(哲學社會科學版),2018(2):160-168.** 55 張協奎,蘇彩虹.中國企業投資高棉基礎設施建設探討.廣西大學學報(哲學社會科學版),2018(2):73-81.* 56 陳茜,張協奎(通訊作者).基於EBA協整分析的廣州市合理房價水平實證研究....
現任自然資源部海底科學重點實驗室主任、中國海洋學會海洋測繪專委會副主任、中國海洋與湖沼學會海洋測繪專委會副主任、中國岩石力學與工程學會海洋工程與地質災害防控分會副理事長、浙江省地質學會副理事長與學術委員會副主任。入選浙江省特級專家、國務院政府特殊津貼專家、國家百千萬人才工程-有突出貢獻中青年專家;全國...
1998/09-2001/12,西北工業大學,工程力學系,博士。工作經歷 1984/07-1987/09,雲南省地震局,地震前兆研究室,助工 1990/08-1996/12,中國地震局,第二地形變監測中心,工程師 1997/01-2002/12, 中國地震局,第二地形變監測中心,高級工程師 2003/01-2004/12,長安大學,地質工程與測繪學院,副教授 2005/...
