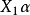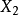協方差分析亦稱“共變數（數）分析”。方差分析的引申和擴大。基本原理是將線性回歸與方差分析結合起來，調整各組平均數和 F 檢驗的實驗誤差項，檢驗兩個或多個調整平均數有無顯著差異，以便控制在實驗中影響實驗效應（因變數）而無法人為控制的協變數（與因變數有密切回歸關係的變數）在方差分析中的影響。例如，在研究某種教學方法（實驗變數）對學業成績（實驗效應）的影響時，被試的原有知識基礎同時影響學業成績，但往往在實驗中難以選取具備相同知識基礎的被試參加實驗，可用協方差分析從學業成績的總變異中將歸因於被試知識基礎差異的部分劃分出去，便於確切地分析教學方法對學業成績的影響，其中被試的知識基礎就是協變數。
基本介紹
定義,套用技巧,意義,方法,回歸模型的協方差分析,相關模型的協方差分析,
定義
協方差分析是研究方差分析模型與回歸模型的一種線性模型：
參數向量α 有一定的約束條件：
是模型的回歸部分，設計矩陣
中變數是連續型的。因為含有兩種類型因素（連續型，屬性型）的混合，故稱之為協方差分析模型。但是這兩部分不能同等對待，主要的還是方差分析部分，而回歸部分只是因某些變數完全人為地控制而不得已引入的。
套用技巧
第一步，由
在某些約束條件下解出的 α,β ，便是協方差模型中參數向量 α,β 的最小二乘估計。
意義
當研究者知道有些協變數會影響因變數，卻不能夠控制和不感興趣時（當研究學習時間對學習績效的影響，學生原來的學習基礎、智力學習興趣就是協變數），可以在實驗處理前予以觀測，然後在統計時運用協方差分析來處理。
方差是用來度量單個變數 “自身變異”大小的總體參數，方差越大，該變數的變異越大；
協方差是用來度量兩個變數之間 “協同變異”大小的總體參數，即二個變數相互影響大小的參數，協方差的絕對值越大，兩個變數相互影響越大。
對於涉及兩個變數的試驗資料，由於每個變數的總變異既包含了“自身變異”又包含了“協同變異”（是指由另一個變數所引起的變異），須採用協方差分析法來進行分析，才能得到正確結論。
方法
回歸模型的協方差分析
如果那些不能很好地進行試驗控制的因素是可量測的，且又和試驗結果之間存在直線回歸關係，就可利用這種直線回歸關係將各處理的觀測值都矯正到初始條件相同時的結果，使得處理間的比較能在相同基礎上進行，而得出正確結論。這一做法在統計上稱為統計控制。
這時所進行的協方差分析是將回歸分析和方差分析結合起來的一種統計分析方法，這種協方差分析稱為回歸模型的協方差分析。
相關模型的協方差分析
方差分析中根據均方MS與期望均方EMS間的關係，可獲得不同變異來源的方差分量估計值；在協方差分析中，根據均積MP與期望均積EMP間的關係，可獲得不同變異來源的協方差分量估計值。
這種協方差分析稱為相關模型的協方差分析。
