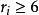半正多面體(semiregular solid) 亦稱“阿基米德體”、“阿基米德多面體”,是由邊數不全相同的正多邊形為面的多面體。如將正方體沿交於一頂點的三條棱的中點截去一個三稜錐,如此共可截去八個三稜錐,得到一個有十四個面的半正多面體,它們的邊都相等,其中八個為正三角形,六個為正方形,稱這樣的半正多面體為二十四等邊體。類似地,若以正方體的各個頂角為圓心,以面之對角線之半為半徑作弧截各邊,每邊得兩交點。依交點於面上作與邊平行的縱橫呈井字形線,共有二十四個交點,即得四十八等邊體之角頂,依各角頂削原體,即成四十八等邊體,設原正方體棱長為a,則四十八等邊體的棱長為a(√2-1)。
基本介紹
- 中文名:半正多面體
- 外文名:semiregular solid
- 所屬學科:數學
- 所屬問題:立體幾何(多面體)
- 別稱:阿基米德體、阿基米德多面體
定義

種類





種類 |  | 面數F | 頂點數V | 棱數E | 體積為1的棱長 |
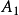 | 3·62 | 8 | 12 | 18 | 0.717 |
 | 3·4·3·4 | 14 | 12 | 24 | 0.445 |
 | 4·62 | 14 | 24 | 36 | 0.263 |
 | 3·82 | 14 | 24 | 36 | 0.419 |
 | 3·5·3·5 | 32 | 30 | 60 | 0.227 |
 | 5·62 | 32 | 60 | 90 | 0.486 |
 | 3·43 | 26 | 24 | 48 | 0.751 |
 | 34·4 | 38 | 24 | 60 | 0.417 |
 | 3·102 | 32 | 60 | 90 | 0.287 |
 | 3·4·5·4 | 62 | 60 | 120 | 0.502 |
 | 4·6·8 | 26 | 48 | 72 | 0.296 |
 | 34·5 | 92 | 60 | 150 | 0.288 |
 | 4·6·10 | 62 | 120 | 180 | 0.169 |






性質