基本介紹
- 中文名：等面半正多面體
- 外文名：isohedral semiregular polyhedron
- 所屬學科：數學
- 所屬問題：立體幾何
- 簡介：一種半正多面體
基本介紹,相關介紹,
基本介紹
等面半正多面體是一種特殊的多面體，指各個面都相等且各個多面角是面數不全相同的正多面角的多面體。等面半正多面體的面最多有五個邊。
例如，公共底對稱的兩個正n稜錐所構成的2n面體——正雙n稜錐就是等面半正多面體，又如過正方體的各棱分別作與各面成45°角的平面，所圍成的多面體稱為十二菱面體(有十二個相等的菱形面，六個正四面角和八個正三面角)，有時叫做斜方十二面體，也是等面半正多面體。
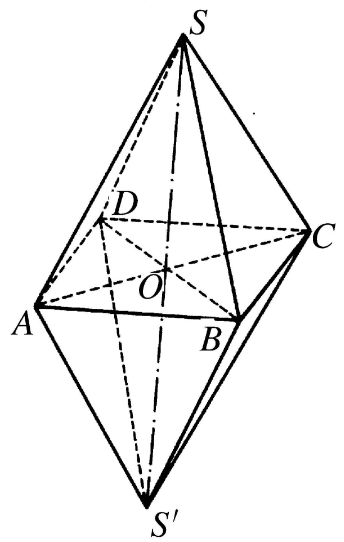圖3如果多面體的面是由幾種不同的正多邊形組成，而它們的多面角都相等，這樣的多面體叫做等角半正多面體。如果多面體的多面角是幾種不同的角度而各面都相等，這種多面體就叫做等面半正多面體。合稱半正多面體。半正多面體是由正多面體演變得來的。
相關介紹
正多面體的概念可以推廣到半正(semiregular) 多面體，從正多面體出發，通過截頂(truncation)、鈍頂(snalling)、仿射(affinity)等方式可以獲得13種等頂半正多面體(所有的頂點都等同地外接於一個球面，但正多邊形不只一種)，這類多面體被稱作Archimeades體。例如：將一個二十面體，沿棱的1/3處，截去所有的頂，就得到一個截頂二十面體，有32個面(12個正五邊形和20個正六邊形)與60個頂點。對這種等頂半正多面體進行對偶化，即頂面互換，外接球變為內切球，可以得到對應的等面半正多面體，例如與截項二十面體相對偶的是相同等腰三角形組成的六十面體，與二十-十二面體相對偶的是菱形(銳角為63.43°，鈍角為116.57°)三十面體。上面提到的這幾種多面體，都保持了二十面體對稱性，參見圖4，值得注意，這裡的兩種等面半正多面體中多邊形都不是正多邊形，但仍然保持了二十面體對稱性。
圖4(a) 截頂二十面體與其對偶六十面體
圖4(b) 二十-十二面體與其對偶菱形三十面體注 圖4：具有二十面體對稱性的幾種半正多面體。
