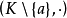基本介紹
- 中文名:半域
- 外文名:semi-field
- 所屬學科:數學
- 屬性:一類結構特殊的半環
- 分類:0一半域、∞一半域
基本介紹,相關概念,半域的定義,半域的分類,
基本介紹
常用的半環記號
首先列出常用的半環記號:




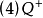


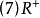
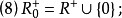

相關概念
定義1 設S是一個半環,若S中元素a具有性質
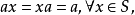
顯然,若S是含零元的交換半換,則S既是S的加法恆等元,又是S的乘法零元,簡稱這樣的半環S為帶零半環。
定義2 若半環S含有一個乘法零元 ,具有性質
,具有性質

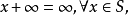

顯然,上面列出的(2)、(5)和(8)是帶零半環,而(3)、(6)和(9)是帶無窮元的半環。
半域的定義
值得注意的是半域K的零元未必是加法恆等元,從而未必是半環K的零元,半域的乘法恆等元將記為1。
每個域是半城,並且上面的半環(5),(6),(8)和(9)均是半域而非域。
半域的分類
定理1 K是一個半域,a是K的零元,那么下面之一成立:
1)對任意 ,有
,有


2)對任意 ,有
,有


證明:首先證明 令
令 則
則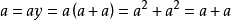 。
。


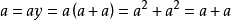
情形1 存在某個 ,
, ,使得
,使得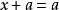 ,對任意
,對任意 那么
那么 故
故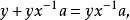 即
即 ,亦即2)成立;
,亦即2)成立;


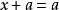


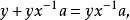

情形2 對所有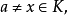 有
有 則
則 設
設 那么
那么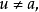 且
且 故存在
故存在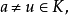 使
使 現在對任意
現在對任意 有
有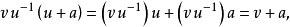 而
而 故
故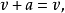 即1)成立。
即1)成立。
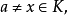



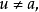

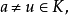


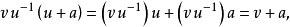

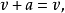
由此定理看出,僅有兩種類型的半域,或者對任意x有 或者對任意x有
或者對任意x有 在第一種情形,a扮演著加法恆等元的角色(通常記此元為0),故我們稱第一種情形的半域為0型半域或0—半域;在第二種情形,a相當於一個加零(通常記為
在第一種情形,a扮演著加法恆等元的角色(通常記此元為0),故我們稱第一種情形的半域為0型半域或0—半域;在第二種情形,a相當於一個加零(通常記為 ),故我們稱第二種類型的半域為無窮元型半域或
),故我們稱第二種類型的半域為無窮元型半域或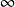 一半域,且記它的零元為
一半域,且記它的零元為 。
。



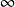

注意:每個域是0一半域, 和
和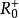 是0一半域而非域,
是0一半域而非域, 和
和 是
是 一半域而非域。
一半域而非域。

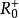



在定理1的證明中,我們證明了如果存在一個非零元x使 那么每個非零元都有這個性質,且如果存在一個非零元x使
那么每個非零元都有這個性質,且如果存在一個非零元x使 那么每個非零元也都有此性質,證明中用到了每個非零元都有乘逆這個事實,這種斷言在半域理論中會經常用到,即如果某個非零元具有某一性質,那么每個非零元均有此性質,我們稱此為半域的一致性原理。(關於半域更多的知識可查閱相應參考資料)。
那么每個非零元也都有此性質,證明中用到了每個非零元都有乘逆這個事實,這種斷言在半域理論中會經常用到,即如果某個非零元具有某一性質,那么每個非零元均有此性質,我們稱此為半域的一致性原理。(關於半域更多的知識可查閱相應參考資料)。