包含關係（inclusionr relotion）是概念外延間關係的一種，通常即指屬種關係。有時也僅僅作為真包含關係和真包含於關係的統稱。一說包含關係還包括概念外延問（或類與類間）的全同關係。即A概念與B概念有包含關係是指： A概念在外延上全同於B概念的關係或A概念包含於B概念的關係。按此，如果A概念與B概念在外延上有全同關係，那么，A概念與B概念有包含關係，即二者互相包含的關係。
基本介紹
- 中文名：包含關係
- 外文名：Contains the relationship
- 學科：數學
- 符號表示：A⊂B
- 屬性：從屬關係
- 相關名詞：真包含、包含於
- 定義：概念外延間關係的一種
簡介,定義,分類,性質,機率名詞,簡介,舉例,
簡介
定義
分類
（1）包含於（包含）
（2）真包含（真包含於）
性質
（1）傳遞性：若集合A包含於集合B，集合B包含於集合C，那么集合A包含於集合C。
（2）歸屬性：集合A包含於集合B，那么集合A在集合B裡面，歸屬於B。
機率名詞
簡介
實際中，在一個隨機現象中常會遇到許多事件，它們之間有下列三種關係。
(1)包含：
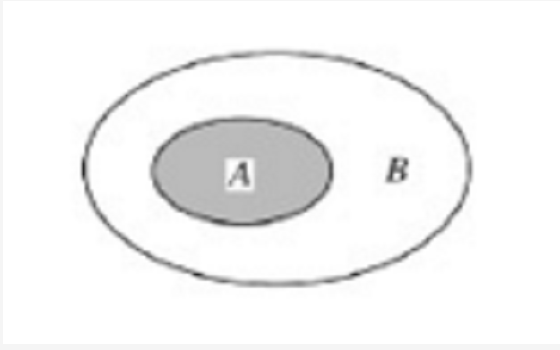
包含關係圖
在一個隨機現象中有兩個事件A與B。若事件A中任一個樣本點必在B中，則稱A被包含在B中，或B包含A，記為“A包含於B”：A⊂B或“B包含A”：B⊃A，這時事件A的發生必導致事件B發生。如右圖所示。如擲一顆骰子，事件A=“出現4點”必導致事件B=“出現偶數點”的發生，故A⊂B。
(2)互不相容：
在一個隨機現象中有兩個事件A與B。若事件A與B沒有相同的樣本點，則稱事件A與B互不相容。這時事件A與B不可能同時發生。如圖1所示，如在電視機壽命試驗里“電視機壽命小於1萬小時”與“電視機壽命超過4萬小時”是兩個互不相容事件，因為它們無相同的樣本點?或者說它們不可能同時發生。
兩個事件間的互不相容性可推廣到三個或更多個事件間的互不相容。例如在檢查三個產品時候，C1=“恰有一件不合格品”，C2=“恰有兩件不合格品”，C3=“全是不合格品”，C0=“沒有不合格品”是四個互不相容事件。
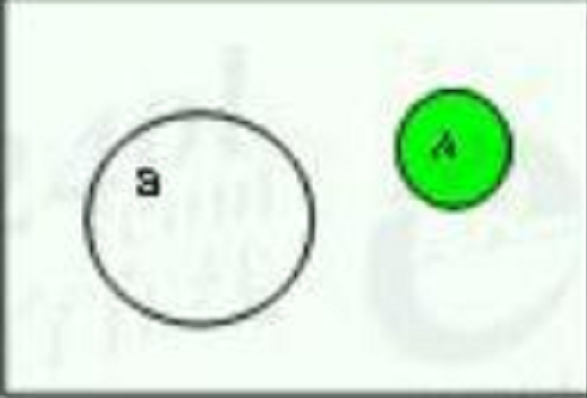
圖1 互不相容
(3)相等:
在一個隨機現象中有兩個事件A與B。若事件A與B含有相同的樣本點，則稱事件A與B相等，記為A=B。如在擲兩顆骰子的隨機現象中，其樣本點記為(x，y)，其中x與y分別為第一與第二顆骰子出現的點數，如下兩個事件:A={(x，y):x+y=奇數}，B={(x，Y):x與y的奇偶性不同}，可以驗證A與B含有相同的樣本點，故A=B。
舉例
元素和集合之間的互相包含的關係叫“屬於”，而不能說成包含，包含只能用於集合與集合之間。
例A={1,2},B={1,2,3}
則1∈A,2∈A,3∈B
屬於是元素和集合之間的關係，例如，元素a屬於集合A，記為a∈A
屬於符號：∈,用於元素與集合之間
集合與集合之間的包含才叫包含
