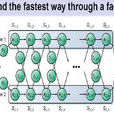
分類 動態規劃一般可分為線性動規,區域動規,樹形動規,背包動規四類。
舉例:
線性動規:攔截飛彈,合唱隊形,挖地雷,建學校,劍客決鬥等;
區域動規:石子合併, 加分二叉樹,統計單詞個數,炮兵布陣等;
樹形動規:貪吃的九頭龍,二分查找樹,聚會的歡樂,數字三角形等;
背包問題:01背包問題,完全背包問題,分組背包問題,二維背包,裝箱問題,擠牛奶(
同濟 ACM第1132題)等;
套用實例:
POJ動態規劃題目列表:
容易:
不易:
推薦:
概念意義 動態規劃問世以來,在經濟管理、
生產調度 、工程技術和
最優控制 等方面得到了廣泛的套用。例如最短路線、庫存管理、資源分配、
設備更新 、排序、裝載等問題,用動態規劃方法比用其它方法求解更為方便。
雖然動態規劃主要用於求解以時間劃分階段的動態過程的最佳化問題,但是一些與時間無關的靜態規劃(如線性規劃、
非線性規劃 ),只要人為地引進時間因素,把它視為多階段決策過程,也可以用動態規劃方法方便地求解。
動態規劃程式設計是對解最最佳化問題的一種途徑、一種方法,而不是一種特殊算法。不像搜尋或數值計算那樣,具有一個標準的數學表達式和明確清晰的解題方法。動態規劃程式設計往往是針對一種最最佳化問題,由於各種問題的性質不同,確定最優解的條件也互不相同,因而動態規劃的設計方法對不同的問題,有各具特色的解題方法,而不存在一種萬能的動態規划算法,可以解決各類最最佳化問題。因此讀者在學習時,除了要對基本概念和方法正確理解外,必須
具體問題具體分析 處理,以豐富的想像力去建立模型,用創造性的技巧去求解。我們也可以通過對若干有代表性的問題的動態規划算法進行分析、討論,逐漸學會並掌握這一設計方法。
概念引入 多階段決策過程的最最佳化問題。
在現實生活中,有一類活動的過程,由於它的特殊性,可將過程分成若干個互相聯繫的階段,在它的每一階段都需要作出決策,從而使整個過程達到最好的活動效果。當然,各個階段決策的選取不是任意確定的,它依賴於當前面臨的狀態,又影響以後的發展,當各個階段決策確定後,就組成一個決策序列,因而也就確定了整個過程的一條活動路線,如圖所示:(看詞條圖)這種把一個問題看作是一個前後關聯具有鏈狀結構的多階段過程就稱為多階段決策過程,這種問題就稱為多階段決策問題。
多階段決策問題 基本思想 動態規划算法通常用於求解具有某種最優性質的問題。在這類問題中,可能會有許多可行解。每一個解都對應於一個值,我們希望找到具有
最優值 的解。動態規划算法與
分治法 類似,其基本思想也是將待求解問題分解成若干個子問題,先求解子問題,然後從
這些子 問題的解得到原問題的解。與分治法不同的是,適合於用動態規劃求解的問題,經分解得到子問題往往不是互相獨立的。若用分治法來解這類問題,則分解得到的子問題數目太多,有些子問題被重複計算了很多次。如果我們能夠保存已解決的子問題的答案,而在需要時再找出已求得的答案,這樣就可以避免大量的重複計算,節省時間。我們可以用一個表來記錄所有已解的子問題的答案。不管該子問題以後是否被用到,只要它被計算過,就將其結果填入表中。這就是動態規劃法的基本思路。具體的動態規划算法多種多樣,但它們具有相同的填表格式。
基本概念 1. 多階段決策問題
如果一類活動過程可以分為若干個互相聯繫的階段,在每一個階段都需作出決策(採取措施),一個階段的決策確定以後,常常影響到下一個階段的決策,從而就完全確定了一個過程的活動路線,則稱它為多階段決策問題。
各個階段的決策構成一個決策序列,稱為一個策略。每一個階段都有若干個決策可供選擇,因而就有許多策略供我們選取,對應於一個策略可以確定活動的效果,這個效果可以用數量來確定。策略不同,效果也不同,多階段決策問題,就是要在可以選擇的那些策略中間,選取一個最優策略,使在預定的標準下達到最好的效果.
2.動態規劃問題中的術語
階段 :把所給求解問題的過程恰當地分成若干個相互聯繫的階段,以便於求解,過程不同,階段數就可能不同.描述階段的變數稱為階段變數。在多數情況下,階段變數是離散的,用k表示。此外,也有階段變數是連續的情形。如果過程可以在任何時刻作出決策,且在任意兩個不同的時刻之間允許有無窮多個決策時,階段變數就是連續的。
在前面的例子中,第一個階段就是點A,而第二個階段就是點A到點B,第三個階段是點B到點C,而第四個階段是點C到點D。
狀態 :狀態表示每個階段開始面臨的自然狀況或客觀條件,它不以人們的主觀意志為轉移,也稱為不可控因素。在上面的例子中狀態就是某階段的出發位置,它既是該階段某路的起點,同時又是前一階段某支路的終點。在前面的例子中,第一個階段有一個狀態即A,而第二個階段有兩個狀態B1和B2,第三個階段是三個狀態C1,C2和C3,而第四個階段又是一個狀態D。
不可控因素 過程的狀態通常可以用一個或一組數來描述,稱為狀態變數。一般,狀態是離散的,但有時為了方便也將狀態取成連續的。當然,在現實生活中,由於變數形式的限制,所有的狀態都是離散的,但從分析的觀點,有時將狀態作為連續的處理將會有很大的好處。此外,狀態可以有多個分量(多維情形),因而用向量來代表;而且在每個階段的狀態維數可以不同。當過程按所有可能不同的方式發展時,過程各段的狀態變數將在某一確定的範圍內取值。狀態變數取值的集合稱為狀態集合。
狀態變數 無後效性 :我們要求狀態具有下面的性質:如果給定某一階段的狀態,則在這一階段以後過程的發展不受這階段以前各段狀態的影響,所有各階段都確定時,整個過程也就確定了。換句話說,過程的每一次實現可以用一個狀態序列表示,在前面的例子中每階段的狀態是該線路的始點,確定了這些點的序列,整個線路也就完全確定。從某一階段以後的線路開始,當這段的始點給定時,不受以前線路(所通過的點)的影響。狀態的這個性質意味著過程的歷史只能通過當前的狀態去影響它的未來的發展,這個性質稱為無後效性。
無後效性 決策 :一個階段的狀態給定以後,從該狀態演變到下一階段某個狀態的一種選擇(行動)稱為決策。在最優控制中,也稱為控制。在許多問題中,決策可以自然而然地表示為一個數或一組數。不同的決策對應著不同的數值。描述決策的變數稱
決策變數 ,因狀態滿足無後效性,故在每個階段選擇決策時只需考慮當前的狀態而無須考慮過程的歷史。
決策變數的範圍稱為允許決策集合。
策略 :由每個階段的決策組成的序列稱為策略。對於每一個實際的多階段決策過程,可供選取的策略有一定的範圍限制,這個範圍稱為允許策略集合。允許策略
允許決策集合 集合中達到最優效果的策略稱為最優策略 。
給定k階段狀態變數x(k)的值後,如果這一階段的決策變數一經確定,第k+1階段的狀態變數x(k+1)也就完全確定,即x(k+1)的值隨x(k)和第k階段的決策u(k)的值變化而變化,那么可以把這一關係看成(x(k),u(k))與x(k+1)確定的對應關係,用x(k+1)=Tk(x(k),u(k))表示。這是從k階段到k+1階段的狀態轉移規律,稱為
狀態轉移方程。 最最佳化原理:作為整個過程的最優策略,它滿足:相對前面決策所形成的狀態而言,餘下的子策略必然構成“最優子策略”。一個問題滿足最最佳化原理也稱其擁有最優子結構性質。最優性原理實際上是要求問題的最優策略的子策略也是最優。讓我們通過對前面的例子再分析來具體說明這一點:從A到D,我們知道,最短路徑是AB1C2D,這些點的選擇構成了這個例子的最優策略,根據最優性原理,這個策略的每個子策略應是最優:
狀態轉移方程 AB1C2是A到C2的最短路徑,B1C2D也是B1到D的最短路徑……──事實正是如此,因此我們認為這個例子滿足最優性原理的要求。
最最佳化原理 基本結構 多階段決策問題中,各個階段採取的
決策 ,一般來說是與時間有關的,決策依賴於當前狀態,又隨即引起狀態的轉移,一個決策序列就是在變化的狀態中產生出來的,故有“動態”的含義,稱這種解決多階段決策最最佳化問題的方法為動態規劃方法。
基本模型 根據上例分析和動態規劃的基本概念,可以得到動態規劃的基本模型如下:
(1)確定問題的決策對象。 (2)對決策過程劃分階段。 (3)對各階段確定
狀態變數 。 (4)根據狀態變數確定費用
函式 和目標函式。 (5)建立各階段狀態變數的轉移過程,確定狀態轉移方程。
狀態轉移方程的一般形式:
一般形式: U:狀態; X:策略
倒推:
適用條件 任何思想方法都有一定的局限性,超出了特定條件,它就失去了作用。同樣,動態規劃也並不是萬能的。適用動態規劃的問題必須滿足最最佳化原理和無後效性。
1.
最最佳化原理 (最優子結構性質) 最最佳化原理可這樣闡述:一個最最佳化策略具有這樣的性質,不論過去狀態和決策如何,對前面的決策所形成的狀態而言,餘下的諸決策必須構成最優策略。簡而言之,一個最最佳化策略的子策略總是最優的。一個問題滿足最最佳化原理又稱其具有最優子結構性質。
2.
無後效性 將各階段按照一定的次序排列好之後,對於某個給定的階段狀態,它以前各階段的狀態無法直接影響它未來的決策,而只能通過當前的這個狀態。換句話說,每個狀態都是過去歷史的一個完整總結。這就是無後向性,又稱為無後效性。
3.子問題的重疊性 動態規劃將原來具有指數級時間複雜度的
搜尋算法 改進成了具有多項式時間複雜度的算法。其中的關鍵在於解決冗餘,這是動態規划算法的根本目的。動態規劃實質上是一種以空間換時間的技術,它在實現的過程中,不得不存儲產生過程中的各種狀態,所以它的空間複雜度要大於其它的算法。
實現問題 算法 實現是比較好考慮的。但有時也會遇到一些問題,而使算法難以實現。動態規劃思想設計的算法從整體上來看基本都是按照得出的
遞推 關係式進行遞推,這種遞推相對於計算機來說,只要設計得當,效率往往是比較高的,這樣在時間上溢出的可能性不大,而相反地,動態規劃需要很大的
空間 以存儲中間產生的結果,這樣可以使包含同一個子問題的所有問題共用一個子問題解,從而體現動態規劃的優越性,但這是以犧牲空間為代價的,為了有效地訪問已有結果,數據也不易壓縮存儲,因而空間矛盾是比較突出的。另一方面,動態規劃的高時效性往往要通過大的測試數據體現出來(以與
搜尋 作比較),因而,對於大規模的問題如何在基本不影響運行速度的條件下,解決空間溢出的問題,是動態規劃解決問題時一個普遍會遇到的問題。
一個思考方向是儘可能少占用
空間 。如從結點的
數據結構 上考慮,僅僅
存儲 必不可少的內容,以及數據存儲範圍上精打細算(按位存儲、壓縮存儲等)。當然這要因問題而異,進行分析。另外,在實現動態規劃時,一個我們經常採用的方法是用一個與結點數一樣多的數組來存儲每一步的決策,這對於倒推求得一種實現最優解的方法是十分方便的,而且處理速度也有一些提高。但是在記憶體空間緊張的情況下,我們就應該抓住問題的主要矛盾。省去這個存儲決策的數組,而改成在從最優解逐級倒推時,再計算一次,選擇某個可能達到這個值的上一階段的狀態,直到推出結果為止。這樣做,在程式編寫上比上一種做法稍微多花一點時間,運行的時效也可能會有一些(但往往很小)的下降,但卻換來了很多的空間。因而這種思想在處理某些問題時,是很有意義的。
但有時,即使採用這樣的方法也會發現空間溢出的問題。這時就要分析,這些保留下來的數據是否有必要同時存在於記憶體之中。因為有很多問題,動態規劃遞推在處理後面的內容時,前面比較遠處的內容實際上是用不著的。對於這類問題,在已經確信不會再被使用的數據上
覆蓋 數據,從而使空間得以重複利用,如果能有效地使用這一手段,對於相當大規模的問題,空間也不至於溢出(為了求出最優方案,保留每一步的決策仍是必要的,這同樣需要空間)。
一般地說,這種方法可以通過兩種思路來實現:一種是遞推結果僅使用Data1和Data2這樣兩個數組,每次將Data1作為上一階段,推得Data2數組,然後,將Data2通過複製覆蓋到Data1之上,如此反覆,即可推得最終結果。這種做法有一個局限性,就是對於遞推與前面若干階段相關的問題,這種做法就比較麻煩;而且,每遞推一級,就需要複製很多的內容,與前面多個階段相關的問題影響更大。另外一種實現方法是,對於一個可能與前N個階段相關的問題,建立數組Data[0..N],其中各項為前面N個階段的保存數據。這樣不採用這種記憶體節約方式時對於階段k的
訪問 只要對應成對數組Data中下標為k mod (N+1)的單元的訪問就可以了。這種處理方法對於程式修改的代碼很少,速度幾乎不受影響,而且需要保留不同的
階段 數也都能很容易實現。
當採用以上方法仍無法解決記憶體問題時,也可以採用對記憶體的動態申請來使絕大多數情況能有效出解。而且,使用動態記憶體還有一點好處,就是在重複使用記憶體而進行交換時,可以只對指針進行交換,而不複製數據,這在實踐中也是十分有效的。
套用 常用軟體 MATLAB、LINGO
作用 在編程中常用解決最長公共子序列問題、
矩陣 連乘問題、凸多邊形最優三角剖分問題、電路布線等問題。
搜尋 記憶化
給你一個數字三角形, 形式如下:
1
2 3
4 5 6
7 8 9 10
找出從第一層到最後一層的一條路,使得所經過的權值之和最小或者最大.
無論對於新手還是老手,這都是再熟悉不過的題了,很容易地,我們寫出狀態轉移方程:
f[i][j]=a[i][j] + min{f[i+1][j],f[i+1][j+1]}(a[i][j]表示當前狀態,f[i][j]表示指標函式)
對於動態規划算法解決這個問題,我們根據狀態轉移方程和狀態轉移方向,比較容易地寫出動態規劃的循環表示方法。但是,當狀態和轉移非常複雜的時候,也許寫出循環式的動態規劃就不是那么簡單了。
解決方法:
我們嘗試從正面的思路去分析問題,如上例,不難得出一個非常簡單的遞歸函式 :
int f(int i, int j, int (*a)[4]){ int f1, f2, tmp=0, k; if(i==0||j==0) return a[0][0]; if(j==i) { for(k=0;k<=i;k++) tmp+=a[k][k]; return tmp; } f1=f(i-1, j, a); f2=f(i-1, j-1, a); if(f1<f2) return f2+a[i][j]; else return f1+a[i][j];} 顯而易見,這個算法就是最簡單的搜尋算法。時間複雜度為2^n,明顯是會逾時的。分析一下搜尋的過程,實際上,很多調用都是不必要的,也就是把產生過的最優狀態,又產生了一次。為了避免浪費,很顯然,我們存放一個opt數組:
Opt[i, j] - 每產生一個f(i, j),將f(i, j)的值放入opt中,以後再次調用到f(i, j)的時候,直接從opt[i, j]來取就可以了。 於是動態規劃的狀態轉移方程被直觀地表示出來了,這樣節省了思維的難度,減少了編程的技巧,而運行時間只是相差常數的複雜度,避免了動態規劃狀態轉移先後的問題,而且在相當多的情況下,
遞歸算法 能更好地避免浪費,在比賽中是非常實用的。
並且記憶搜尋占的記憶體相對來說較少。
計算核心片段:
for(inti=n-1;i>=1;--i)//從倒數第二行開始{ for(intj=1;j<=i;j++) { if(a[i+1][j][1]>a[i+1][j+1][1])//左邊大 { a[i][j][2]=0;//選擇左邊 a[i][j][1]+=a[i+1][j][1]; } else//右邊大 { a[i][j][2]=1;//選擇右邊 a[i][j][1]+=a[i+1][j+1][1]; } 練習題
USACO2.2 Subset Sums
題目如下:
對於從1到N的連續整數集合,能劃分成兩個子集合,且保證每個集合的數字和是相等的。
舉個例子,如果N=3,對於{1,2,3}能劃分成兩個子集合,他們每個的所有數字和是相等的:
{3}and {1,2}
這是唯一一種分法(交換集合位置被認為是同一種劃分方案,因此不會增加劃分方案總數)
如果N=7,有四種方法能劃分集合{1,2,3,4,5,6,7},每一種分發的子集合各數字和是相等的:
{1,6,7} and {2,3,4,5} {注 1+6+7=2+3+4+5}
{2,5,7} and {1,3,4,6}
{3,4,7} and {1,2,5,6}
{1,2,4,7} and {3,5,6}
給出N,你的程式應該輸出劃分方案總數,如果不存在這樣的劃分方案,則輸出0。程式不能預存結果直接輸出。
PROGRAM NAME: subset
INPUT FORMAT
輸入檔案只有一行,且只有一個整數N
SAMPLE INPUT (file subset . in)
7
OUTPUT FORMAT
輸出劃分方案總數,如果不存在則輸出0。
SAMPLE OUTPUT (file subset.out)
4
參考程式如下(C++語言):
#include<fstream>usingnamespacestd;constunsignedintMAX_SUM=1024;intn;unsignedlonglongintdyn[MAX_SUM];ifstreamfin("subset.in");ofstreamfout("subset.out");intmain(){fin>>n;fin.close();ints=n*(n+1);if(s%4){fout<<0<<endl;fout.close();return0;}s/=4;inti,j;dyn[0]=1;for(i=1;i<=n;i++)for(j=s;j>=i;j--)if(j-i>0){dyn[j]+=dyn[j-i];}fout<<(dyn[s]/2)<<endl;fout.close();return0;}USACO2.3LongestPrefix 題目如下:
在
生物學 中,一些生物的結構是用包含其要素的大寫字母序列來表示的。生物學家對於把長的序列分解成較短的(稱之為元素的)序列很感興趣。
如果一個集合 P 中的元素可以通過並運算(允許重複;並,即∪,相當於 Pascal 中的 “+” 運算符)組成一個序列 S ,那么我們認為序列 S 可以分解為 P 中的元素。並不是所有的元素都必須出現。舉個例子,序列 ABABACABAAB 可以分解為下面集合中的元素:
{A, AB, BA, CA, BBC}
序列 S 的前面 K 個字元稱作 S 中長度為 K 的前綴。設計一個程式,輸入一個元素集合以及一個大寫字母序列,計算這個序列最長的前綴的長度。
PROGRAM NAME: prefix
INPUT FORMAT
輸入數據的開頭包括 1..200 個元素(長度為 1..10 )組成的集合,用連續的以空格分開的字元串表示。字母全部是大寫,數據可能不止一行。元素集合結束的標誌是一個只包含一個 “.” 的行。集合中的元素沒有重複。接著是大寫字母序列 S ,長度為 1..200,000 ,用一行或者多行的字元串來表示,每行不超過 76 個字元。
換行符 並不是序列 S 的一部分。
SAMPLE INPUT (file prefix. in)
A AB BA CA BBC
.
ABABACABAABC
OUTPUT FORMAT
只有一行,輸出一個整數,表示 S 能夠分解成 P 中元素的最長前綴的長度。
SAMPLE OUTPUT (file prefix.out)
11
示例程式如下:
#include <stdio.h>
#define MAXP 200
#define MAXL 10
char prim[MAXP+1][MAXL+1];
int nump;
int start[200001];
char data[200000];
int ndata;
int main(int argc, char **argv)
{
FILE *fout, *fin;
int best;
int lv,lv2, lv3;
if ((fin = fopen("prim. in", "r")) == NULL)
{
perror ("fopen fin");
exit(1);
}
if((fout = fopen("prim.out", "w")) == NULL)
{
perror ("fopen fout");
exit(1);
}
while (1)
{
fscanf (fin, "%s", prim[nump]);
if (prim[nump][0] != '.')
nump++;
else
break;
}
ndata = 0;
while (fscanf (fin, "%s", data+ndata) == 1)
ndata += strlen(data+ndata);
start[0] = 1;
best = 0;
for (lv = 0; lv < ndata; lv++)
if (start[lv])
{
best = lv;
for (lv2 = 0; lv2 < nump; lv2++)
{
for (lv3 = 0; lv + lv3 < ndata && prim[lv2][lv3] == data[lv+lv3]; lv3++)
if (!prim[lv2][lv3])
start[lv + lv3] = 1;
}
}
if (start[ndata])
best = ndata;
fprintf (fout, "%i\n", best);
return 0;
}
動態規劃作為一種重要的信息學競賽算法,具有很強的靈活性。以上提供的是一些入門練習題,深入的學習還需要逐步積累經驗。
解決0-1背包問題時使用動態規劃的實現(c++)
#include <stdio.h>
typedef struct Object{
int weight;
int value; // float rate;
}
Object;
Object * array; //用來存儲物體信息的數組
int num; //物體的個數
int container; //背包的容量
int ** dynamic_table; //存儲動態規劃表
bool * used_table; //存儲物品的使用情況
//ouput the table of dynamic programming, it's for detection
void print_dynamic_table(){
printf("動態規劃表如下所示:\n");
/* for(int j=0; j<=container; j++) printf("%d ",j); printf("\n");*/
for(int i=1; i<=num; i++) {
for(int j=0; j<=container; j++)
printf("%d ",dynamic_table[i][j]);
printf("\n");
}
}
//列印動態規劃表
void print_array(){
for(int i=1; i<=num; i++)
printf("第%d個物品的重量和權重:%d %d\n",i,array[i].weight,array[i].value);
}
//列印輸入的物品情況//插入排序,按rate=value/weight由小到大排//動態規劃考慮了所有情況,所以可以不用排序
/*void sort_by_rate(){
for(int i=2; i<=num; i++) {
Object temp=array[i];
for(int j=i-1; j>=1; j--)
if(array[j].rate>temp.rate)
array[j+1]=array[j];
else break;
array[j+1]=temp;
}}*/
void print_used_object(){
printf("所使用的物品如下所示:\n");
for(int i=1; i<=num; i++)
if(used_table[i]==1)
printf("%d-%d\n", array[i].weight, array[i].value);
}
//列印物品的使用情況
/* 做測試時使用
void print_used_table(bool * used_table){
printf("used table as follows:\n");
for(int i=1; i<=num; i++)
printf("object %d is %d", i, used_table[i]);
}*/
void init_problem(){
printf("輸入背包的容量:\n");
scanf("%d", &container);
printf("輸入物品的個數:\n");
scanf("%d", &num);
array=new Object[num+1];
printf("輸入物品的重量和價值, 格式如:4-15\n");
for(int i=1; i<=num; i++) {
char c;
scanf("%d%c%d", &array[i].weight, &c, &array[i].value);
// array[i].rate=array[i].value/array[i].weight;
}
print_array();
}
//對物體的使用情況進行回查
void trace_back(){
int weight=container;
used_table=new bool[num+1];
for(int i=1; i<=num; i++) used_table[i]=0;
//initalize the used_table to be non-used
for(int j=1; j<num; j++) {
//說明物品j被使用
if(dynamic_table[j][weight]!=dynamic_table[j+1][weight]) {
weight-=array[j].weight;
used_table[j]=1;
}
// print_used_table(used_table);
}
//檢測第num個物品是否被使用
if(weight>=array[num].weight)
used_table[num]=1;
}
void dynamic_programming(){
dynamic_table=new int * [num+1];
for(int k=1; k<=num; k++)
dynamic_table[k]=new int[container+1];
//dynamic_programming table
//為二維動態規劃表分配記憶體
for(int m=1; m<num; m++)
for(int n=0; n<=container; n++)
dynamic_table[m][n]=0;
int temp_weight=array[num].weight;
for(int i=0; i<=container; i++)
dynamic_table[num][i]=i<temp_weight?0:array[num].value;
//初始化動態規劃表
for(int j=num-1; j>=1; j--) {
temp_weight=array[j].weight;
int temp_value=array[j].value;
for(int k=0; k<=container; k++)
if(k>=temp_weight && dynamic_table[j+1][k] < dynamic_table[j+1][k-temp_weight]+temp_value)
dynamic_table[j][k]=dynamic_table[j+1][k-temp_weight]+temp_value;
else dynamic_table[j][k]=dynamic_table[j+1][k];
}//構建動態規劃表
print_dynamic_table();//列印動態規劃表
}
void main(){
init_problem();
dynamic_programming();
trace_back();
print_used_object();
}
推薦書籍 《Dynamic Programming》
ISBN: 3540370137
 多階段決策問題
多階段決策問題 不可控因素
不可控因素 狀態變數
狀態變數 無後效性
無後效性 允許決策集合
允許決策集合 狀態轉移方程
狀態轉移方程 最最佳化原理
最最佳化原理