加法定理一個是指機率的加法定理,講的是互不相容事件或對立事件甚至任意事件的機率計算方面的公式;另一個是指三角函式的加法定理。
基本介紹
- 中文名:加法定理
- 外文名:addition theorem
- 所屬學科:數學
- 義項:機率加法定理、三角函式加法定理
機率的加法定理
互不相容事件的加法定理
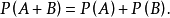
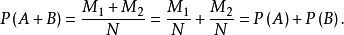
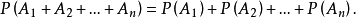
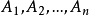
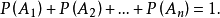
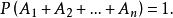

一般的機率加法定理

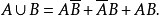

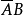


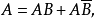

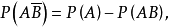

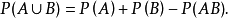

有限個事件情況
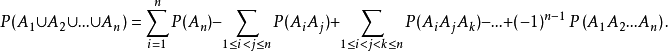
三角函式的加法定理
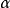
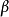
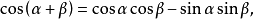

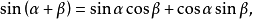


加法定理一個是指機率的加法定理,講的是互不相容事件或對立事件甚至任意事件的機率計算方面的公式;另一個是指三角函式的加法定理。
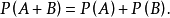
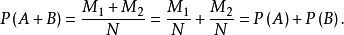
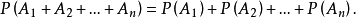
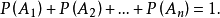
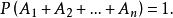


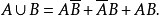

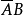


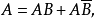

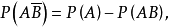

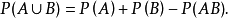

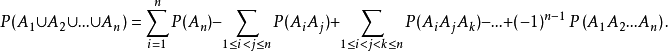
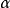
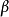
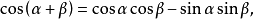

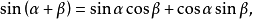

加法定理一個是指機率的加法定理,講的是互不相容事件或對立事件甚至任意事件的機率計算方面的公式;另一個是指三角函式的加法定理。...
加法原理是分類計數原理,常用於排列組合中,具體是指:做一件事情,完成它有n類方式,第一類方式有M1種方法,第二類方式有M2種方法,……,第n類方式有Mn種方法,那么...
加法運算定律指的是交換兩個加數的位置,和不變。...... 加法運算定律結合律 編輯 先把前兩個數相加,或者把後兩個數相加,和不變,這叫做加法結合律。...
一般加法定理(general addition theorem)刻畫一種特殊方程存在連續的非零解特徵的一個定理一般加法定理如下:如果方程 f (x+y>=F(f(二),f<y))(1)在(一二,...
維數加法定理(addition theorem of dimension)關於維數的一組定理: 1.若X,Y為可度量化空間的可分子空間,則 ind <XUY)鎮ind X十ind Y十1. 這是圖馬基(...
加法原理:類類獨立;乘法原理:步步相關。...... 區分兩個原理。要做一件事,完成它若是有n類辦法,是分類問題,第一類中的方法都是獨立的,因此使用加法原理;做一...
,做第n步有mn種不同的方法。那么完成這件事共有 N=m1×m2×m3×…×mn 種不同的方法。 和加法原理是數學機率方面的基本原理。...
計數原理是數學中的重要研究對象之一,分類加法計數原理、分步乘法計數原理是解決計數問題的最基本、最重要的方法,也稱為基本計數原理,它們為解決很多實際問題提供了...
阿貝爾定理:1.如果冪級數在點x0處(x0不等於0)收斂,則對於適合不等式|x|<|x0|的一切x使這冪級數絕對收斂。2.反之,如果冪級數在點x1處發散,則對於適合不...
圖書簡介《排列組合與容斥原理》是蘇州大學出版社出版的一本圖書。內容簡介本書討論了中學生需要掌握的加法原理、乘法原理、組合數與二項式定理,參加數學競賽同學需要...
加號,是用來表示正數或者加法數學符號。此符號還因為各種相對其他事物的類似之處而被賦予了豐富的抽象含義。加號屬於第一級運算。...
和角公式又稱三角函式的加法定理是幾個角的和(差)的三角函式通過其中各個角的三角函式來表示的關係。三角函式是數學中屬於初等函式中的超越函式的一類函式。...
加號是用來表示正數或者加法數學符號。此符號還因為各種相對其他事物的類似之處而被賦予了豐富的抽象含義。加號屬於第一級運算。...
原理 加法原理和乘法原理 特點 排列與元素的順序有關 目錄 1 排列數 2 排列數公式 ▪ 公式 ▪ 符號 ▪ 推導過程 3 基本理論 4 特點 排列...
形如f(x+y)=f(x)+f(y)的方程 相關概念 一般加法定理 目錄 1 基本介紹 2 一般加法定理 加性函式方程基本介紹 編輯 形如的...
