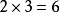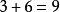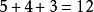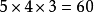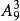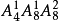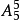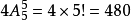原理介紹
加法原理是分類計數原理,常用於排列組合中,具體是指:做一件事,完成它可以有
類方法,在第一類方法中有
種不同方法,在第二類方法中有
種不同方法,……,在第
類方法中有
種不同方法,那么完成這件事共有
種不同的方法。
乘法原理
做一件事,完成它需要分成
個步驟,做第一步有
種不同方法,做第二步有
種不同方法,……,做第
步有
種不同方法,那么完成這件事共有
種不同的方法。
聯繫
加法原理和
乘法原理是兩個基本原理,它們的區別在於一個與分類有關,另一個與分步有關。運用以上兩個原理的關鍵在於
分類要恰當,分步要合理。分類必須包括所有情況,又不要交錯在一起產生重複,要依據同一標準劃分;而分步則應使各步依次完成,保證整個事件得到完成,不得多餘、重複,也不得缺少某一步驟。
例題
分類計數原理、分步計數原理,回答的都是有關做一件事的不同方法種數的問題。兩者區別在於:分類計數原理針對的是“分類”問題,其中各種方法相互獨立,用其中任何一種方法都可以做完這件事;分步計數原理針對的是“分步”問題,各步驟中的方法相互依存,只有各個步驟都完成才算做完這件事。兩個計數原理滲透了“以簡馭繁、化難為易”的基本思想。
簡單問題
例1.如圖,從甲地到乙地有兩條路可走,從乙到丙地有三條路可走,又從甲地不經乙地直達丙地有三條路可走,問從甲地到丙地的不同走法有幾種?
 圖1
圖1解:
第一類從甲直接到丙的有3種,第二類從甲經乙到達丙的有
種,因此從甲到丙地有
種不同的走法。
例2.書架上有不同的數學書5本,不同的物理書4本,不同的化學書3本。
(1)從中任取一本,有多少種不同的取法?
(2)從中每種各取一本,有多少種不同的取法?
分析:
(1)因為從數學、或從物理、或從化學這三類書的任一類中任取一本,都可一次性獨立完成“從中任取一本”這件事,即可分類完成,因此可用加法原理。
(2)因為在這裡不能一步到位,而需分三步進行才能完成。也就是在5本數學中取一本,還要從4本物理書與3本化學中各取一本,才能完成這件事,因此用乘法原理。
解:
有關數字問題
例3. 用0-9這10個數字,可以組成多少個沒有重複數字的4位偶數?
分析:
這一問題的限制條件是:①沒有重複數字;②數字0不能排成在千位數上;③個位數字只能是0、2、4、6、8
從限制條件人手,可劃分如下:
如果從個位數人手,4位偶數可分為:個位數是0的4位偶數;個位數是2、4、6、8的4位偶數(0不能放在千位數上);
如果從千位數入手,4位偶數可分為:千位數是1、3、5、7、9和千位數是2、4、6、8兩類。
如果4位數劃分為4位奇數和4位偶數兩類,先求出4位奇數的個數,用排除法可得解。
解:
當個位數上排0時,千位、百位、十位上可以從餘下的9個數字中任選3個來排列,故有
個;當個位在“2、4、6、8”中任選一個來排,則千位上從餘下的8個非零數字中任選1個,百位、十位上再從餘下的8個數字中任選2個來排,按分步計數原理有
個
數字排列問題對培養學生分析問題、解決問題的能力大有好處,本題是典型的具有簡單條件的排列問題,上述解法是最基本、最常見的解法,要認真體會每種解法的實質,掌握其解答方法,以期靈活運用。
關於工作分配問題
例4. 在奧運會的開幕式表演期間,某一安檢部門有6種不同工作要分配給6人擔任,每個人只擔任一種工作,且甲不能擔任其中某2種工作,問有幾種分配方法?
分析:本題是排列組合中的一道典型問題,根據題意“甲不能擔任其中某2種工作”,其基本解法有直接法、排除法等。
解:
先滿足特殊元素甲,甲能擔任的工作有4種,先分配甲,分配後,餘下工作由其餘5人分擔,有
種分擔方法,故共有分配方法數

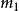
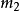

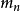
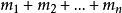

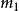
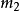

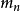
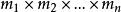
 圖1
圖1