基本介紹
- 中文名：功效函式
- 外文名：power function
- 別名：勢函式
- 套用領域：數理統計
引入,定義,性質,
引入
在進行假設檢時，我們要確立原假設和備擇假設，為了選擇哪種假設，我們規定了拒絕域。如果樣本落在拒絕域內，我們拒絕原假設，接受備擇假設，否則接受原假設。這樣我們在套用某種檢驗做判斷時，可能會犯如下兩種錯誤：原假設是對的，我們卻拒絕了原假設，這稱為第一類錯誤；相反，原假設是錯的，我們卻接受了原假設，這稱為第二類錯誤。在檢驗中我們希望犯兩類錯誤的機率都儘可能地小，但實際上我們做不到這一點，為了說明原因，我們需要引進功效函式這一概念。
定義
設某檢驗問題的拒絕域為W，則樣本觀測值X落在拒絕域W內的機率稱為該檢驗的功效函式，記為
，
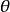為原假設和備擇假設中的參數。
性質
當原假設成立時，犯第一類錯誤的機率就等於。當備擇假設成立時，犯第二類錯誤的機率就等於
。
下面我們通過一個例子來說明我們無法使一個檢驗犯第一類、第二類錯誤的機率同時減少。
某廠生產的合金強度服從常態分配
，其中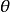
的設計值為不低於110
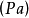。為保證質量，該廠每天都要對生產情況做例行檢查，以判斷生產是否正常進行，即該合金的平均強度不低於110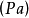。某天從生產的產品中隨機抽取25塊合金，測得其強度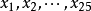值為
，均值為
，問當日生產是否正常。
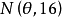
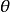
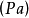
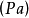
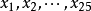
對於本例，其拒絕域為
注意到這個功效函式是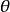的減函式，如右圖利用這個功效函式易得犯兩類錯誤的機率分別為
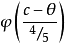（原假設成立），
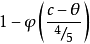（備擇假設成立）。
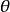
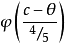
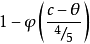
勢函式
勢函式由此可以得出犯兩類錯誤的機率之間的關係：
1、當第一類錯誤的機率減少時，c隨之減小，而c的減小必導致犯第二類錯誤的機率增大。
2、當第二類錯誤的機率減少時，c隨之增大，而c的增大必導致犯第一類錯誤的機率增大。
這一現象說明：兩類錯誤的一個減小必導致另一個的增大。
