劉維爾公式是一個關於多重積分、歐拉第一積分(貝塔函式)和歐拉第二積分(伽瑪函式)的公式。
基本介紹
- 中文名：劉維爾公式
- 外文名：Liouville's Formula
- 提出者：Joseph Liouville
- 套用學科：數學、物理學
公式形式
多重積分中的劉維爾公式如圖1所示。
圖1
劉維爾公式
相關詞條
- 劉維爾公式
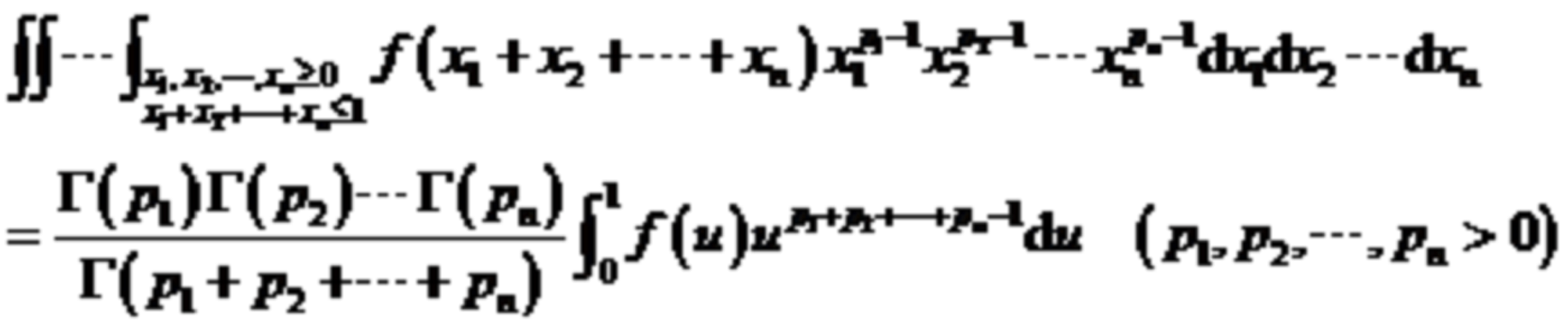
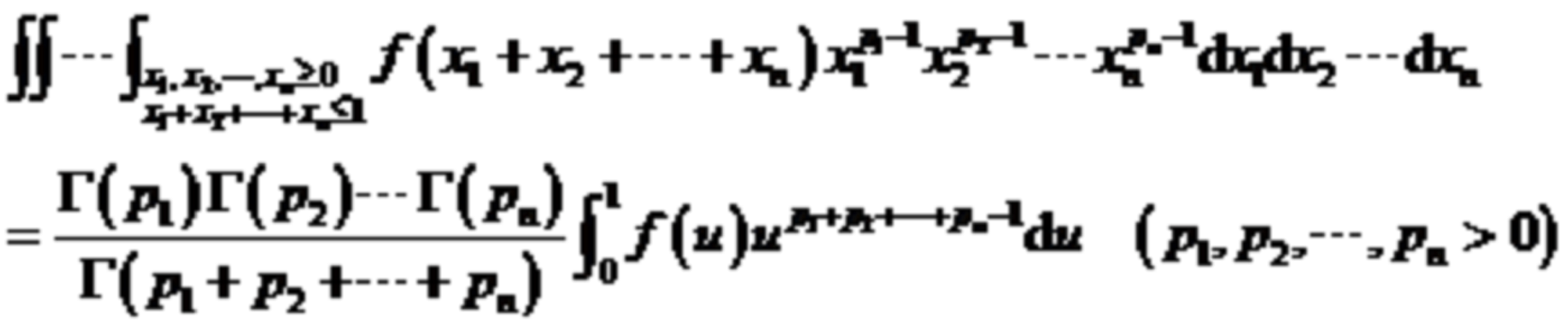
劉維爾公式是一個關於多重積分、歐拉第一積分(貝塔函式)和歐拉第二積分(伽瑪函式)的公式。公式形式多重積分中的劉維爾公式如圖1所示。...
- 一元五次方程求根公式
法國數學家劉維爾（Liouville）閱讀了伽羅瓦的論文後，驚喜地發現伽羅瓦在論文中給出了代數方程可解性的最終判定，而且獨創了一個嶄新的數學概念：群。伽羅瓦工作的核心部分是可解性判別準則：若且唯若多項式方程的群是可解群（伽羅瓦群）...
- 二階常係數線性齊次微分方程
。根據齊次線性微分方程解的性質，方程的通解為 兩個相等實根 設這個實根為 ，則 於是方程有特解 。根據劉維爾公式，與之線性無關的一個解為：於是，方程的通解為：兩個共軛復根 設這對復根為 ，於是方程的通解為：
- 調和函式
劉維爾定理 如果f在整個R都有定義的調和函式，並且在其上有最大值或最小值，那么函式f是常數函式（參見複平面上函式的劉維爾定理）。推廣 調和函式研究的一個推廣是黎曼流形上的調和形的研究，後者與上同調的研究有關。此外，可以定義...
- 高等數學(三)
3、降階法與劉維爾公式 4、二階常係數齊次線性微分方程 第五講 常係數非齊次線性微分方程 1、問題引入 2.1、常係數非齊次線性微分方程——右端函式 2.2、常係數非齊次線性微分方程——右端函式 2.3、常係數非齊次線性微分方程—...
- 微分運算元
: P是一個稠定運算元。例子 施圖姆-劉維爾運算元是形式自伴運算元一個熟知的例子。這個二階微分運算元L可以寫成如下形式 這個性質可用上面的形式自伴的定義來證明。相關條目 差分運算元 Delta operator 橢圓型運算元 分數微積分 不變微分運算元 ...
- 從空間曲線到高斯-博內定理
第四部分討論了曲面上的測地線,測地方程,以及歐拉公式,羅德里格斯公式,與恩尼珀定理等。在本書的後一章——第十章中,證明了計算測地曲率的劉維爾公式,並用它證明了閉曲面的高斯-博內定理。據此,引入閉曲面的歐拉示性數,證明它是一個...
