基本介紹
- 中文名:劈錐曲面
- 外文名:conoid
- 所屬學科:數學(立體幾何)
- 性質:一種曲面
- 分類:拋物劈錐曲面、圓劈錐曲面
基本介紹
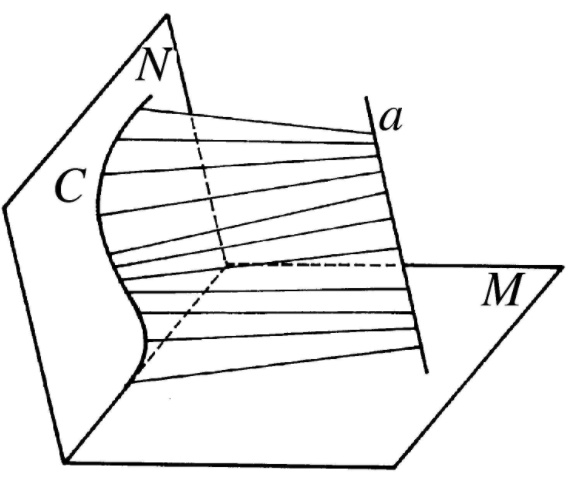 圖1
圖1兩種劈錐曲面
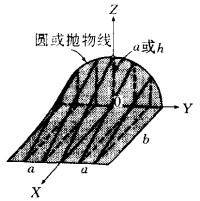 圖2 圖2 | 項點為  直紋曲面由準曲線      |
項點為  直紋曲面由準曲線  直線     |
拋物劈錐曲面

















 圖3 典型的拋物劈錐曲面
圖3 典型的拋物劈錐曲面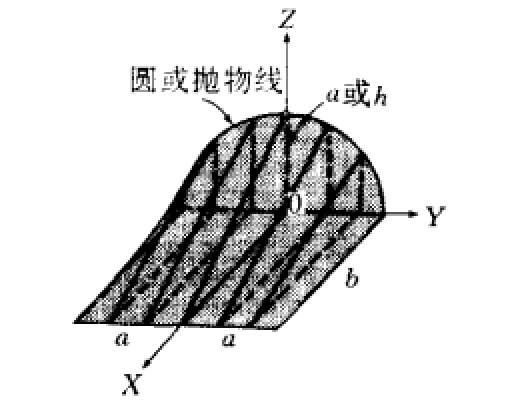
 圖1
圖1 圖2 圖2 | 項點為  直紋曲面由準曲線      |
項點為  直紋曲面由準曲線  直線     |

















 圖3 典型的拋物劈錐曲面
圖3 典型的拋物劈錐曲面設A為與三維向量空間E相關聯的仿射空間,D為A的仿射直線,P為E的平面,稱與D相交且平行於P的仿射直線的並所構成的曲面C為以D為軸以P為方向平面的劈錐曲面(...
劈錐一種特殊的擬柱體,指導向曲線封閉的劈錐曲面,被平行於其導向直線的平面所截得的封閉立體。劈錐曲面是一種曲面,它是由一條平行於已知平面(方向平面)且和...
《劈錐曲面與迴轉橢圓體》 作者:【古希臘】 阿基米德,共32個命題,研究橢圓的面積以及迴轉圓錐曲線體被平面截取部分的體積等。...
論劈錐曲面體與迴轉橢圓體(On Conoids andSpheroids)古希臘數學著作.希臘數學家、物理學家、天文學家阿基米德(Archimedes)著.是作者在有關由曲線和曲面所圍成的...
導向曲線封閉的劈錐曲面和滿足下述條件的兩平行平面所圍成的封閉立體,稱為對棱劈錐:1.兩平行平面與劈錐曲面的導向直線平行,且與所有的母線均相交。2.導向直線...
劈錐曲面被導向直線分成的兩部分,稱為劈錐曲面的兩葉,劈錐曲面的每一葉,稱為半劈錐曲面。...
圓劈錐曲面(circular conoid)是一種特殊的劈錐曲面,指導向曲線是一個圓的劈錐曲面,圓劈錐曲面的導向曲線稱為導向圓。劈錐曲面是一種曲面,它是由一條平行於...
共28個命題,前10個是關於圓及切線的各種比例關係的.命題11重新證明了自然數平方和的不等式,這在《劈錐曲面與迴轉橢圓體》中是作為引理提出。...
)的學生或朋友,與阿基米德(Archimedes)關係甚密,並將阿基米德的著作傳送給亞歷山大的學者.阿基米德的《拋物線圖形求積法》、《論球與圓柱》、《劈錐曲面與迴轉橢圓體...
《論劈錐曲面體與球體》《拋物線求積》《論螺線》西方哲學家盧梭 編輯 西方哲學家基本信息 (Jean-Jacques Rousseau,1712年6月28日——1778年7月2日)是瑞士兼法...
如命題9:“在所有球缺中,與半球具有相同表面積者體積最大。”作者在前言中談到了他關於螺線與劈錐曲面體的發現,並準備在以後的著作中敘述。...
阿基米德的著述很多 ,流傳下來的有《 論球與圓柱》、《 圓的度量》、《劈錐曲面與旋轉橢圓體》、《論螺線》、《拋物線圖形求積法》、《平面圖形的平衡或其重心...
