基本介紹
由一端在曲線上,另一端在一直線上滑移一直線段所形成的曲面稱為劈錐曲面(圖1,2)。 劈錐曲面根據它的端曲線是圓弧、拋物線還是橢圓弧而分別稱為圓劈錐曲面、拋物線劈錐曲面或橢圓劈錐曲面。劈錐曲面是一種鞍形曲面,它的主曲率線說明在端曲線頂點到對角的連線方向的曲率是向上的,而另一主曲串是向下的(圖2)。 劈錐曲面可用作以曲線端為固定端的懸臂殼,此時常使橫向曲率朝上(圖3)。
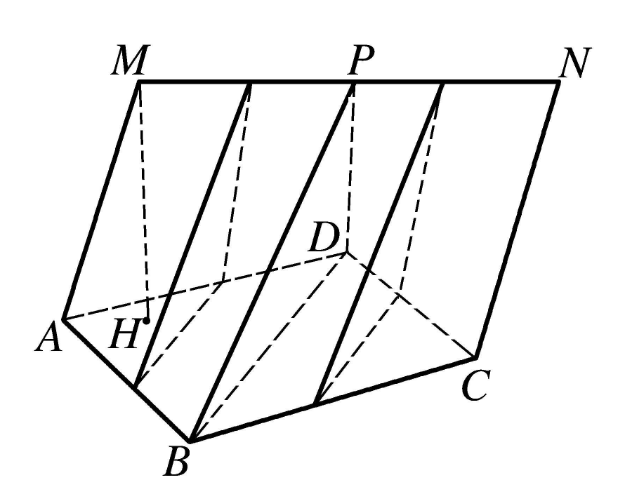
劈錐一種特殊的擬柱體,指導向曲線封閉的劈錐曲面,被平行於其導向直線的平面所截得的封閉立體。其中:截面稱為劈錐的底面;導向直線交於劈錐的線段,稱為劈錐的頂棱;頂棱和底面間的距離,稱為劈錐的高;劈錐曲面的母線(直線)夾在劈錐的頂棱、底面間的線段,稱為劈錐的母線;劈錐曲面夾在劈錐的頂棱、底面間的部分,稱為劈錐的側面。底面是圓的劈錐稱為圓劈錐。圖中劈錐MN-ABCD的底面是平行四邊形ABCD;MN為頂棱;MH⊥面ABCD,H為垂足,MH為劈錐的高線,其長度為劈錐體的高,MA,PB等均是劈錐的母線,曲面MABP,PBCN,NCDP,PDAM都是劈錐的側面。
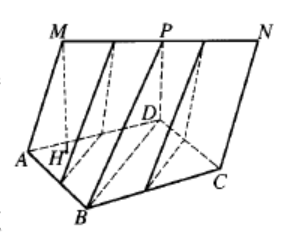 圖1
圖1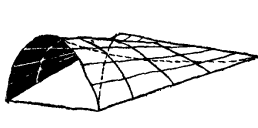 圖2
圖2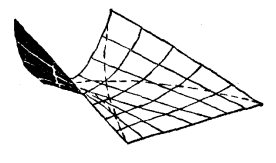 圖3
圖3相關介紹
直紋曲面是一直線依某種規律移動所產生的曲面,動直線叫做母線;與母線移動的軌跡相交的某一定曲線(通常可取平面曲線)叫做準曲線,簡稱準線,設準線C為參數方程是p=p (u)(u1≤u≤u2),經過準線上各點的母線上的單位向量為τ=τ(u)(u1≤u≤u2),則直紋曲面向量形式的參數方程為:P=p (u) +vτ (u) (u1≤u≤u2,-∞<v<+∞),其中v是參數,其意義是直紋曲面上的點P沿母線到準線的有向線段的大小,直紋曲面的坐標形式的參數方程是:x=f (u) +vl (u),y=g (u) +v m (u),z=h (u) +v n (u) (u1≤u≤u2,-∞<v<+∞)。
兩端在兩條各別的曲線上滑動的直線線段所形成的任何曲面稱為直紋曲面。當兩曲線是在空間的兩條相對傾斜直線時,直紋曲面就是
雙曲拋物面,雙曲拋物面具有位於曲面上的一對直線族。柱面是由在兩條相同的平行豎曲線上滑移一水平直線而形成的直紋曲面。
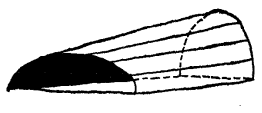 圖4 截錐曲面
圖4 截錐曲面在平行平面內的兩條不同的曲線上滑移一直線段,可形成一族不同的直紋曲面,這類曲面稱為截錐曲面。截錐曲面屋頂覆蓋矩形平面,且可以讓光線從給定方向(通常是從北面)進入室內(圖4)。
由一端在曲線上,另一端在一直線上滑移一直線段所形成的曲面稱為劈錐曲面(圖2)。劈錐曲面根據它的端曲線是圓弧、 拋物線還是橢圓弧而分別稱為圓劈錐曲面、拋物線劈錐曲面或橢圓劈錐曲面。劈錐曲面是一種鞍形曲面,它的主曲率線說明在端曲線頂點到對角的連線方向的曲率是向上的,而另一主曲率是向下的(圖2)。劈錐曲面可用作以曲線端為固定端的懸臂殼,此時常使橫向曲率朝上(圖3)。
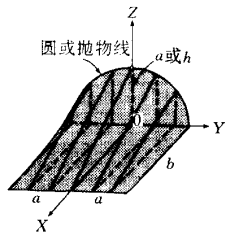 圖5劈錐曲面 圖5劈錐曲面 | 頂點為O 直紋曲面由準曲線 (圓)、準直線x=b,z= 0(平行於y軸的直線),和準平面y=0(xz平面)確定。 (A) (B) |
頂點為V直紋曲面由準曲準 (拋物線)、準直線x=b,z=0(平行於y軸的直線)和準平面y=0(xz平面)確定。 (A) (B) |
錐形曲面是直線段的一端繞一點轉動而另一端在曲線上滑動所形成的直紋曲面。 錐扇形曲面(圖6)屬於截錐曲面的範疇,可用以覆蓋梯形平面,或者象劈錐曲面那樣用作懸臂屋頂。
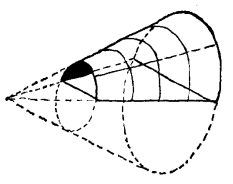 圖6 錐扇形曲面
圖6 錐扇形曲面一傾斜直線段在兩個具有公共圓心軸的水平圓上滑移, 所形成的曲面稱為單葉雙曲面,它的豎截面為雙曲線的兩支(圖7)。這種易於成型的曲面廣泛地用於水泥廠和其它工廠的冷卻塔。
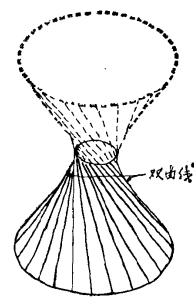 圖7 單頁雙曲面
圖7 單頁雙曲面 圖1
圖1 圖2
圖2 圖3
圖3 圖4 截錐曲面
圖4 截錐曲面 圖5劈錐曲面
圖5劈錐曲面





 圖6 錐扇形曲面
圖6 錐扇形曲面 圖7 單頁雙曲面
圖7 單頁雙曲面