基本介紹
綜述
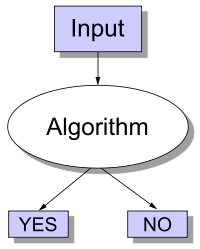 決定性問題只有是-否兩種輸出
決定性問題只有是-否兩種輸出判定性問題一般指本詞條
 決定性問題只有是-否兩種輸出
決定性問題只有是-否兩種輸出在可計算性理論與計算複雜性理論中,所謂的決定性問題(Decision problem)是一個在某些形式系統回答是或否的問題。例如:“給兩個數字x與y,x是否可以整除y?”便是決定性問題,此問題可回答是或否,且依據其x與y的值。綜述 決定性...
70年代以來,通過研究命題邏輯的判定方法的複雜性,發現了許多已知的組合型的判定問題都可化歸為命題邏輯的判定問題,如果能找到判定命題邏輯中的公式是否為重言式的快速算法,則可隨之而獲得一大批判定問題的快速算法。但迄今這仍是懸案,既...
(2)評價潛在問題的危險性,即按其危險度對潛在問題進行排隊分類。(3)制定預防措施。即根據危險度的分類,決定是否採取預防措施和應該採取哪些預防措施,並把這些措施列入決策方案的實施計畫中去,使之逐項落實。(4)準備應急措施,對可能...
判定問題 CSPs也研究計算複雜性問題和有限模型理論. 一個重要的問題是,是否為每一組的關係、套都可視為CSPs選自只使用關係設定不是在p 或 NP-完全問題. 如果這樣一個二分法真實可靠, 那么CSPs提供已知的最大的一個NP 子集,避免...
波斯特對應問題是一個重要的判定問題,提出者是美籍波蘭數學家E.L.波斯特,提出時間是1944年。波斯特對應問題在形式語言理論和程式設計理論中有重要套用。概念 波斯特對應問題是一種不可判定性問題。一個波斯特對應系統是由一個字母表A和A...
這是一個不可判定問題列表。目錄 1 邏輯問題 2 抽象電腦(Abstract machine)問題 3 矩陣問題 4 組合群論(combinatorial group theory)問題 5 拓撲學問題 6 可解答性問題 7 其它問題
第10到第12問題 (10)能否通過有限步驟來判定不定方程是否存在有理整數解?求出一個整數係數方程的整數根,稱為丟番圖(約210-290,古希臘數學家)方程可解。1950年前後,美國數學家戴維斯(Davis)、普特南(Putnan)、羅賓遜(...
我們對任何一種輸入都預期會有單一個輸出,但是輸出不像是決定性問題一樣這么單純。換句話說,輸出不只YES跟NO。重要的範例像是旅行推銷員問題,詢問一張圖是否有可以繞過每一點的不重複路徑(輸出為路徑),以及整數分解,輸出為輸入...
更精確地說,它嘗試將問題分成能或不能在現有的適當受限的資源條件下解決這兩類。相應地,在現有資源條件下的限制正是區分計算複雜性理論和可計算性理論的一個重要指標:後者關心的是何種問題原則上可以用算法解決。決定性問題 在可...
當我們系統地思考問題時,會從多個角度看待同一個問題,蒐集並評估儘可能多的信息,並詳細地研究不同方案可能產生的影響。常見的啟發式判斷方法有代表性啟發法、可得性啟發法和錨定效應。常見啟發式判斷方法 代表性啟發法 在使用啟發式...
§4.2 全等三角形的判定及其套用 §4.3 特殊三角形的判定問題 §4.4 探究三角形性質舉例 §4.5 有關特殊四邊形的問題 習題四 第五章 相似形與解直角三角形 §5.1 平行線與比例線段的關係的探究 §5.2 平行線與三角形面積...
素性判別是判別給定的正整數是否素數的簡稱,不僅具有很大的理論意義,而且更具有重要的套用價值。簡介 判別給定的正整數是否素數簡稱素性判別。素性判別是數論中一個基本而古老的問題,對它的研究,不僅具有很大的理論意義,而且由於近代...
