分層建模,是將多輸入多輸出建模問題分解為一系列單輸入多輸出的數據建模問題,提高多輸入多輸出系統建模的效率和準確性。該模型適宜描述結構複雜的系統,可以包含較多的輸入變數,有利於充分利用現有的系統的信息。
基本介紹
- 中文名:分層建模
- 外文名:layered modeling
- 學科:控制科學與工程
- 適用系統:多輸入複雜系統
- 基本釋義:分解系統為多個單入單出問題
- 優勢:更具普遍性
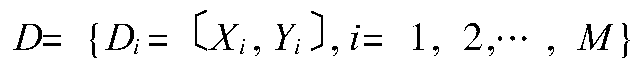




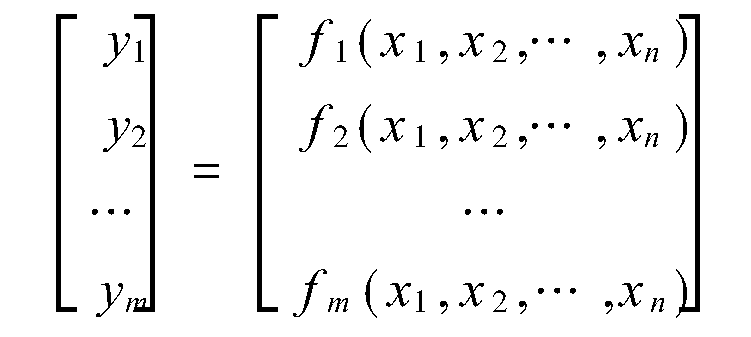



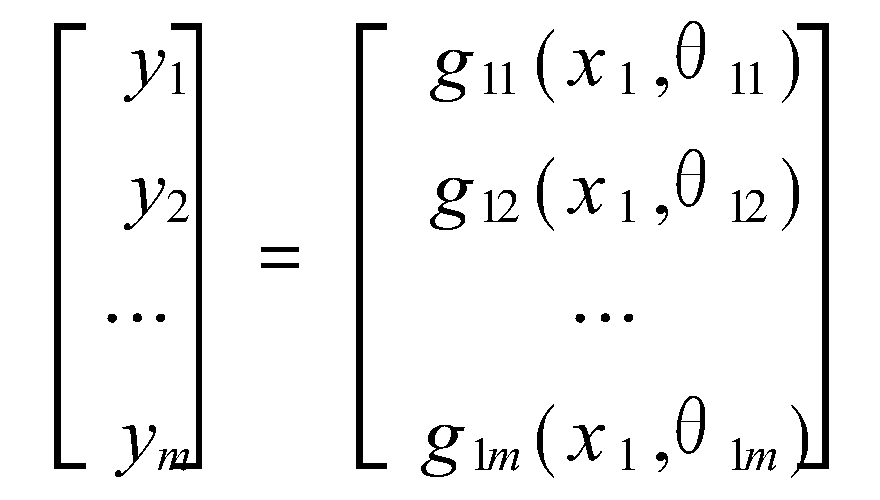

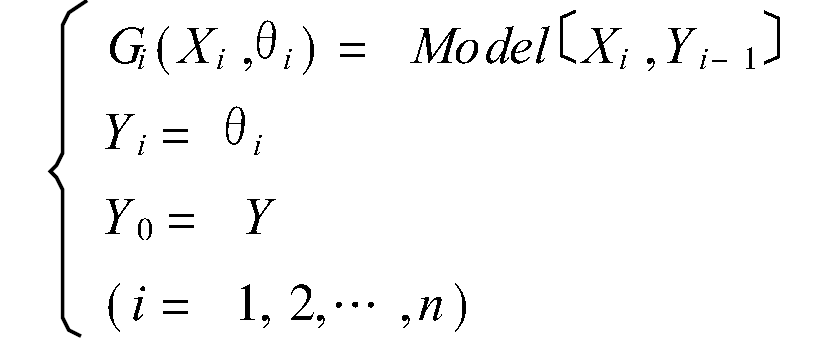
算法結構







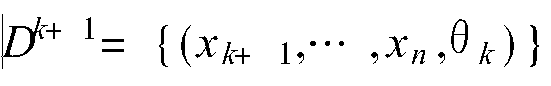
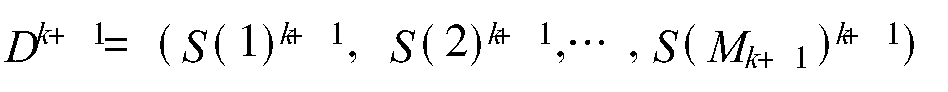
θk+ 1= Yk
優點


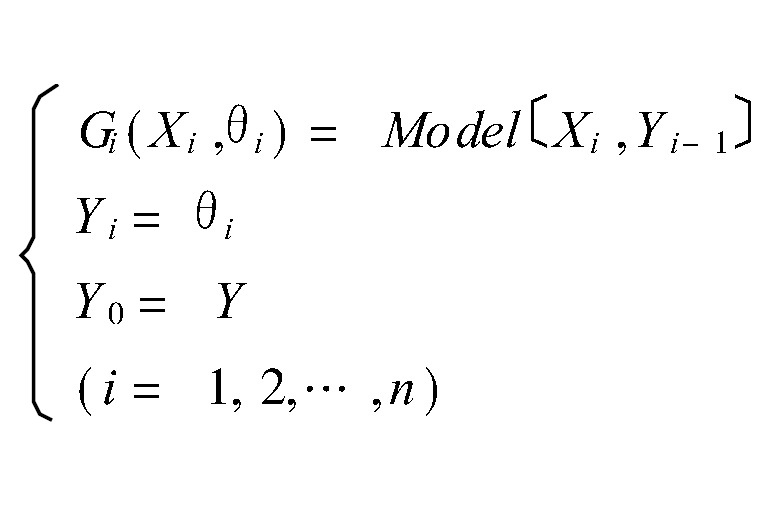
分層建模,是將多輸入多輸出建模問題分解為一系列單輸入多輸出的數據建模問題,提高多輸入多輸出系統建模的效率和準確性。該模型適宜描述結構複雜的系統,可以包含較多的輸入變數,有利於充分利用現有的系統的信息。
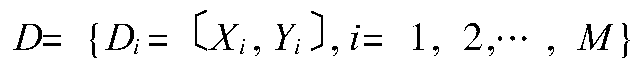




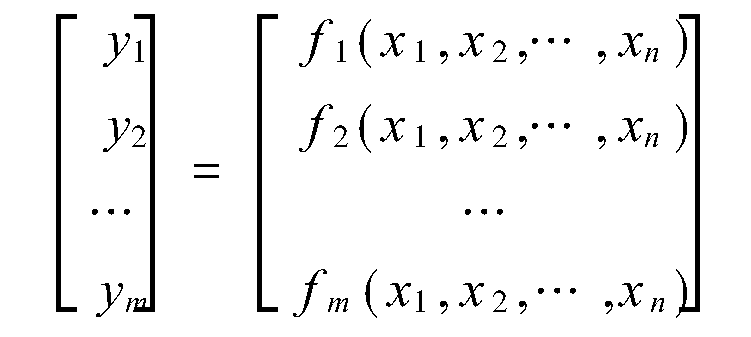



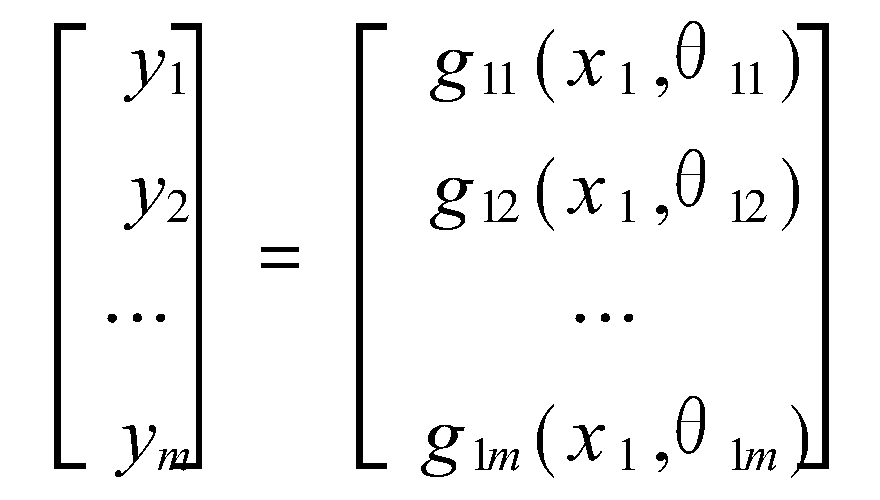

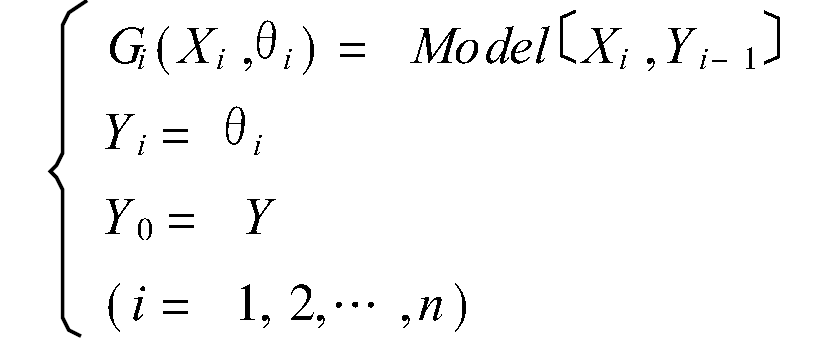







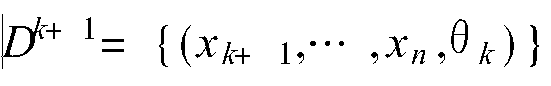
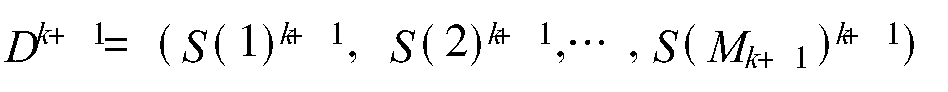


分層建模,是將多輸入多輸出建模問題分解為一系列單輸入多輸出的數據建模問題,提高多輸入多輸出系統建模的效率和準確性。該模型適宜描述結構複雜的系統,可以包含較多的輸入變數,有利於充分利用現有的系統的信息。
由於單一的巨大的協定會加大網路設計難度,同時也不利於分析查找問題 分層模型是一種用於開發網路的設計方法,描述了通信問題劃分為幾個小的問題(層次),每個問 題對應一個層次 所謂分層設計方法就是照信息的流動過程將網路的整體功能...
雖然第1版主要是討論層-1結果變數為連續分布的情況,然而現在的第 2版的第三部分中又包括了一系列其他類型結果變數的分析,比如: 新的第10章介紹分層模型在結果變數為二分類變數、計數變數、序次變數以及多項分類變數條件下的套用,...
《景物分層模型建立中的視覺算法進化研究》是依託清華大學,由朱志剛擔任項目負責人的青年科學基金項目。基本信息 項目摘要 景物分層表示是基於內容的視頻壓縮和檢索、基於圖象的虛擬環境建模的核心方法。本項目擬以自然景物的運動序列建立符合...
多層次模型是使用多層次數據闡述不同層級間關係的統計技術。在過去的幾十年間,多層次模型的統計基礎在各學科內發展起來,並被給予不同的稱謂,包括分層線性模型、隨機係數模型、混合效應模型、協方差結構模型以及增長曲線模型等。所有這些...
Bachman 參加了ANSI早期的會議,並提交了他的七層模型,這個模型就成了提交ISO專委會的唯一的一份草案。1978年3月,在ISO的OSI專委會在華盛頓召開的會議上,與會專家很快達成了共識,認為這個分層的體系結構能夠滿足開放式系統的大多數...
在這個分層結構中,測試自動化代碼被分成三層:(1)測試用例層,表達應用程式的測試邏輯。(2)領域層,用業務領域術語來給待測系統建模,封裝HTTP請求、瀏覽器控制、結果解析邏輯等,給測試用例層提供一個接口。(3)待測系統層,第2...
邏輯分層模型是指在不同的管理層應該實現哪些功能組,同一範疇的管理功能可能在不同的層次實現,但管理的目標和範圍是不同的,其在高層主要實現企業一級目標的管理,在低層主要實現一個具體網路、一個網元的管理。邏輯分層模型將TMN的...
(1)資料庫系統的分層設計。(2)網路分層體系結構。(3)作業系統分層體系結構。舉例 開放系統互連參考模型 (Open System Interconnect 簡稱OSI)是國際標準化組織(ISO)和國際電報電話諮詢委員會(CCITT)聯合制定的開放系統互連參考模型,為開放...
採用分層線性模型能解決層次數據或多水平數據的統計分析問題,而克服了採用傳統的統計分析方法(傳統的線性模型)分析多水平數據導致分析推斷錯誤的缺點。分層線性模型分析方法已逐漸形成了一個新分支,其內容已超出了傳統的統計範圍。
似乎ruby on rails就是這種模型,他甚至把domain object和DAO都合併了。 該模型優點: 1、簡化了分層 2、也算符合OO 該模型缺點: 1、很多不是domain logic的service邏輯也被強行放入domain object ,引起了domain ojbect模型的不穩定 2、...
分層模型統計理論的發展簡史………5 分層線性模型的早期套用………6 個體效應的改進估計………6 對層次之間效應的建模………7 分解方差協方差成分………9 本書第1版問世以來的新發展 ………...
選擇數據存儲技術(如關係、分層或索引存儲技術)。 一定要知道建模通常會以意想不到的方式涉及公司的管理。例如,當對哪些數據元素應由哪些組織來維護有新的見解時,數據所有權(以及數據維護、準確性和及時性的隱含責任)通常會遭到質疑。數...
選擇數據存儲技術(如關係、分層或索引存儲技術)。一定要知道建模通常會以意想不到的方式涉及公司的管理。例如,當對哪些數據元素應由哪些組織來維護有新的見解時,數據所有權(以及數據維護、準確性和及時性的隱含責任)通常會遭到質疑。
網際網路協定棧共有五層:套用層、傳輸層、網路層、鏈路層和物理層。不同於OSI七層模型這也是實際使用中使用的分層方式。(1)套用層 支持網路套用,套用協定僅僅是網路套用的一個組成部分,運行在不同主機上的進程則使用套用層協定進行...
如果觀測涉及不同的學校,同時考慮不同的學校變數,則構成一個三水平模型。學生水平嵌套於班級水平,班級水平嵌套於學校...這樣的數據具有兩個水平,第一水平是學生,第二水平是班級,學生嵌套於到級之中,稱之為分層數據。
14.3 分層模型 141 14.4 一個小最佳化 142 14.5 抽取後驗 142 14.6 討論 144 14.7 練習 144 第 15章 處理多維問題 145 15.1 臍部細菌 145 15.2 獅子,老虎和熊 145 15.3 分層版本 148 15.4 隨機抽樣 149 15.5 ...
1 EPON簡介 2 EPON分層模型 ▪ 1 EPON數據鏈路層 ▪ 2 EPON物理層 ▪ 3 各層之間的接口 EPON簡介 EPON(Ethernet Passive Optical Network)以太無源光網路,是一種新型的光纖接入網技術,它採用點到多點結構、無源光纖傳輸...
模型中的包和子系統,代表一個分層結構。通過關聯關係“represents”擁有,或通過聚合關係“owns”遞歸擁有。類和封裝體模型中的類和封裝體,由包擁有。通過聚合關係“owns”遞歸擁有。接口和協定模型中的接口和協定,由包擁有。通過聚合關係...
這種分層體系結構具有以下四個優點:(1)避免了表示層直接訪問數據訪問層,表示層只和業務邏輯層有聯繫,提高了數據安全性。(2)有利於系統的分散開發,每一個層可以由不同的人員來開發,只要遵循接口標準,利用相同的對象模型實體類就...
層次分析法比較適合於具有分層交錯評價指標的目標系統,而且目標值又難於定量描述的決策問題。基本原理 層次分析法根據問題的性質和要達到的總目標,將問題分解為不同的組成因素,並按照因素間的相互關聯影響以及隸屬關係將因素按不同層次...
層次分析模型 編輯 將問題包含的因素分層:最高層(解決問題的目的);中間層(實現總目標而採取的各種措施、必須考慮的準則等。也可稱策略層、約束層、準則層等);最低層(用於解決問題的各種措施、方案等)。把各種所要考慮的因素放在適當...
層次結構(hierarchy)是一種作業系統的組織結構,其提供了一種隔離作業系統各層功能的模型。其包括歸屬層次結構 dissonance-attribution hierarchy維度層次結構 dimension hierarchy層次結構資料庫 hierarchical database等。...
