凸規劃對偶問題(dual problem of convex pro-gramming)一類綜合的對偶問題.指線性規劃、帶凸性的非線性規劃和二次規劃的對偶問題的綜合形式.
基本介紹
- 中文名：凸規劃對偶問題
- 外文名：dual problem of convex pro-gramming
- 所屬學科：數學
套用
例如，若二次規劃問題的矩陣形式是
公式
則其對偶問題是
公式
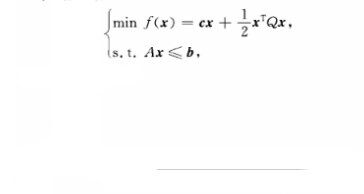
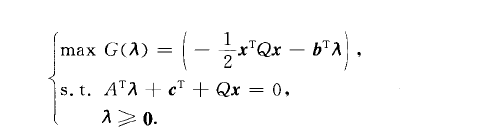
凸規劃對偶問題(dual problem of convex pro-gramming)一類綜合的對偶問題.指線性規劃、帶凸性的非線性規劃和二次規劃的對偶問題的綜合形式.
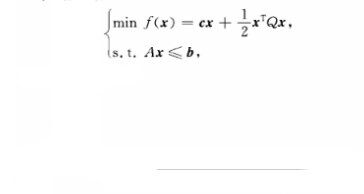
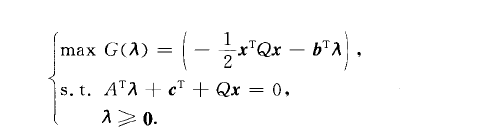
凸規劃對偶問題(dual problem of convex pro-gramming)一類綜合的對偶問題.指線性規劃、帶凸性的非線性規劃和二次規劃的對偶問題的綜合形式.套用例如，若二次規劃問題的矩陣形式是則其對偶問題是...
多目標凸規劃 多目標凸規劃（multiobjective convex program- ming）是1993年公布的數學名詞。公布時間 1993年，經全國科學技術名詞審定委員會審定發布。出處 《數學名詞》第一版。
4.3精確懲罰 ——序貫二次規劃 4.3.1不可微精確罰函式 4.3.2可微精確罰函式 4.4拉格朗日方法和原始-對偶內點法 4.4.1一階方法 4.4.2等式約束問題的類牛頓方法 4.4.3全局收斂性 4.4.4原始-對偶內點法 4.4.5不同方法的比較 4.5注釋和參考資料 第 5章對偶性與凸規劃 5.1對偶問題 5.1.1幾何...
本項目以凸規劃的基礎理論和算法為基礎，研究了大規模凸非對稱矩陣最佳化的有效算法，並研製了相應的Matlab程式，其代表性結果可歸納如下： 1. 針對大規模矩陣核範數最佳化問題，研究了求解該問題的可實現的迫(鄰)近點算法框架，該算法框架包含了原始、對偶以及原始-對偶三種不同形式的迫近點算法。基於算法編制的軟體包PPA...
2.1 線性規劃問題的標誰型 2.2 基本解和基本可行解 2.3 線性規劃的基本定理 2.4 基本可行解與極點的關係 習題 第三章 單純形法 3.1 最優基本可行解的判斷 3.2 基本可行解的改進 3.3 單純形法概述 3.4 初始基本可行解的確定 3.5 退化情況與Bland法則 習題 第四章 對偶線性規劃 4.1 對偶線性規劃...
1.2.1 凸集和凸函式 1.2.2 凸規劃問題及其基本性質 1.2.3 凸規劃的對偶理論 1.2.4 凸規劃的最優性條件 1.2.5 線性規劃 1.3 Hilbert空間上的凸規劃 1.3.1 凸函式及Frechet導數 1.3.2 凸規劃問題 1.3.3 凸規劃的對偶理論 1.3.4 凸規劃的最優性條件 1.4 歐式空間上帶有廣義不等式...
1984年發表論文，”多目標凸規劃的自身對偶性”。1984年至1987年，任中國運籌學會第二屆理事。1985年發表論文，“自身對偶數學規劃問題的推廣”。1985年發表論文，“多目標非線性規劃對偶理論的推廣”。1987年發表論文，“多目標非凸規劃解的充分必要條件”。1988年至1991年，任中國運籌學會第三屆理事。1988年發表論文...
4.3.1 凸規劃問題的標準形式 4.3.2 局部最佳化和全局最佳化 4.3.3 最優性條件 4.3.4 解的性質 習題 第5章 線性規劃 5.1 線性規劃問題的標準形式 5.1.1 標準形式 5.1.2 一般形式到標準形式的轉換 5.1.3 線性規劃套用問題 5.2 線性規劃問題的解 5.3 線性規劃問題解的性質 5.4 線性規劃求解的...