凍結曲線(freezing curve)是指水溶液冷卻後凍結時的溶液溫度與時間的關係曲線。生物的凍結曲線,主要是用來研究小型個體或組織塊等的過冷能力和凍結過程。
基本介紹
- 中文名:凍結曲線
- 外文名:freezing curve
- 定義:水溶液冷卻後凍結時的溶液溫度
- 主要目的:小型個體或組織塊等的過冷能力
概念介紹
曲線介紹
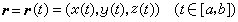 公式一
公式一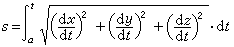 公式二
公式二凍結曲線(freezing curve)是指水溶液冷卻後凍結時的溶液溫度與時間的關係曲線。生物的凍結曲線,主要是用來研究小型個體或組織塊等的過冷能力和凍結過程。
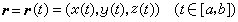 公式一
公式一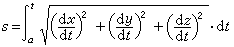 公式二
公式二凍結曲線(freezing curve)是指水溶液冷卻後凍結時的溶液溫度與時間的關係曲線。生物的凍結曲線,主要是用來研究小型個體或組織塊等的過冷能力和凍結過程。...
食品凍結溫度曲線是食品在冷卻、凍結過程中,食品溫度與所經歷的時間關係曲線。...... 凍結曲線食品在緩慢凍結的過程中,水分隨溫度而變化。以牛肉薄片的凍結曲線為例,...
食品凍結溫度曲線,是衡量食品在凍結過程中溫度隨時間變化關係的曲線。隨著凍結的進行,食品溫度在逐漸下降。不論何種食品其溫度曲線在性質上都是相似的。曲線可分為三...
食品在凍結過程中,溫度逐漸下降,食品溫度與凍結時間關係的曲線。...... 食品在凍結過程中,溫度逐漸下降,食品溫度與凍結時間關係的曲線。中文名 速凍溫度曲線 外文名...
凍結溫度(freezing temperature; solidification point),是判斷土是否處於凍結狀態的指標。當降至某一溫度時,食品中的水分開始凍結,並形成冰晶,這個溫度即為食品的凍結...
熱力致死速率曲線表示某一種特定的菌在特定條件下和特定的溫度下,其總的數量隨殺菌時間的延續所發生的變化。...
“凍結磁場”是天文學專有名詞。來自中國天文學名詞審定委員會審定發布的天文學專有名詞中文譯名,詞條譯名和中英文解釋數據著作權由天文學名詞委所有。補充說明“英漢...
“時間凍結”(Time Freeze)是套用於影視製作中的一種特殊視覺效果, 它首先採用照相機陣列(往往採用傳統的模擬單眼相機構成) , 以被攝體為中心, 將照相機按一定...
磁凍結定理(theorem of frozen-in field) 闡述理想導電流體和磁場一起運動的規律的定理,即①開爾文定理:通過和理想導電流體一起運動的任意封閉曲線所圍面積的磁感應...
食品凍藏是套用製冷技術使食品快速凍結並保持在凍結狀態下貯藏的食品保藏方法。...... 冰晶大小和膠體濃縮是影響凍結食品質量的重要因素。凍結曲線食品在緩慢凍結的過程...
55℃的管架式空氣凍結產品的凍結曲線相近,由於魚體大,體重從幾十公斤到幾百公斤,凍結至魚體中心溫度-18℃需要2~3天時間,從而影響到魚體質量,而快速凍結,又易...
通過對鹽漬土在低溫下試驗,鹽潰土的凍結過程和普通土一樣,分冷卻及過冷、溫度突變、水結晶和繼續冷卻四個階段。土(砂)隨著溫度的降低達到起始凍結溫度以後,土層...
