基本介紹
- 中文名:典型相關分析
- 外文名:canonical correlation analysis
- 領域:統計學
- 套用:整體相關性分析
簡介
定義

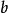
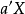
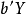
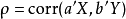
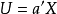

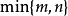
計算
1.求導
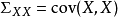
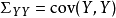
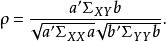
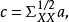
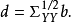
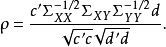
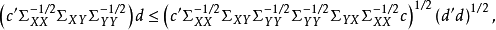
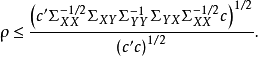
2.解法

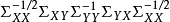
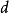
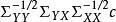
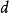
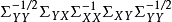



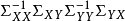
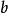
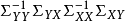

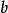
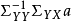
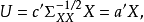
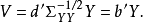

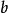
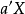
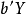
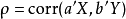
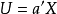

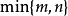
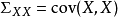
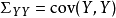
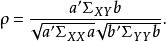
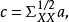
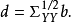
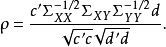
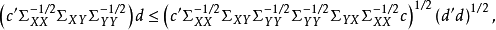
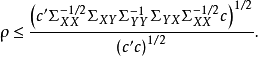

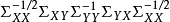
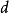
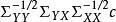
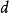
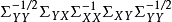



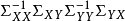
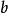
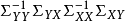

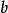
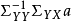
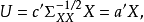
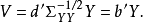
典型相關分析(canonical correlation analysis),是對互協方差矩陣的一種理解,是利用綜合變數對之間的相關關係來反映兩組指標之間的整體相關性的多元統計分析方法。它的...
重要的多元統計分析方法有:多重回歸分析(簡稱回歸分析)、判別分析、聚類分析、主成分分析、對應分析、因子分析、典型相關分析、多元方差分析等。...
編寫的教材,內容涉及常用統計數據分析的基本內容與方法,包括數據的描述性分析、線性回歸分析、方差分析、主成分分析和典型相關分析、判別分析、聚類分析、Bayes統計分析...
因子分析的基本目的就是用少數幾個因子去描述許多指標或因素之間的聯繫,即將相關比較密切的幾個變數歸在同一類中,每一類變數就成為一個因子,以較少的幾個因子反映...
(常稱為因素分析或變數的篩選);第三個任務(也稱相關分析)是在固定(或稱消除)...用樣本估計線性回歸模型中未知常數的方法也很多,經典的方法為最小二乘法,它的...
《多變數分析方法》是2005年中國稅務出版社出版的圖書,作者是陳正昌。該書主要講述了多元回歸分析、典型相關分析等分析方法。...
用以研究確定的自變數與因變數之間的關係;②判別函式分析和聚類分析,用以研究對事物的分類;③主成分分析、典型相關和因素分析,研究如何用較少的綜合因素代替為數...
思考與練習第15章 典型相關分析§15.1 典型相關分析的基本理論§15.2 典型相關分析的步驟及邏輯框圖§15.3 典型相關分析的上機實現思考與練習...
第一節 線性典型相關分析 一、什麼是線性典型相關分析 二、線性典型相關分析的思路 三、線性典型相關分析所需要的SPSS程式 四、線性典型相關分析的主要輸出結果 第二...
12.4 對應分析圖習題第十三章 典型相關分析13.1 引言13.2 總體典型相關13.3 樣本典型相關13.4 典型相關係數的顯著性檢驗習題附錄一 習題參考答案...
本書是在高等院校非數學類專業機率論與數理統計必修課內容基礎上編寫的以介紹實用數理統計方法為目的的教材。內容包括:多元回歸分析、主成分分析及典型相關分析、判別...
