共軛矢量空間(conjugate vector space)是共軛與復向量空間的空間。
基本介紹
- 中文名:共軛矢量空間
- 外文名:conjugate vector space
- 適用範圍:數理科學
簡介
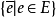
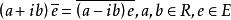
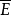
性質

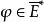
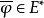
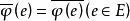
共軛矢量空間(conjugate vector space)是共軛與復向量空間的空間。
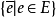
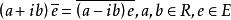
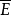

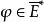
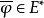
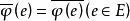
共軛矢量空間(conjugate vector space)是共軛與復向量空間的空間。...... 共軛矢量空間(conjugate vector space)是共軛與復向量空間的空間。中文名 共軛矢量空間 外...
在數學上,內積空間是增添了一個額外的結構的矢量空間。這個額外的結構叫做內積或...即C實現了H與H*之間的保范共軛線性同構,在此同構意義下,把fy與y視為等同,...
共軛叢向量叢 編輯 向量叢是一個幾何構造,對於拓撲空間(或流形,或代數簇)的每一點用互相兼容的方式附上一個向量空間,所用這些向量空間"粘起來"就構成了一個新...
L空間都是巴拿赫空間,但只有當p= 2的時候,L空間是希爾伯特空間。也就是說,可以為L空間中的元素定義內積。表示複數的共軛。這個內積是從2-範數自然誘導的內積。L...
組成。子空間,與 等價,由只有前 元素是非零 的所有 元組組成。的兩個向量在模去這個子空間的同一個共軛類中若且唯若他們的後 個坐標相等。商空間 / 顯然地...
該書可供對空間解析幾何的愛好者以及有志於研究數學的大學生、研究生、教師及...4.2 輪換矢量4.2.1 定義4.2.2 公式4.2.3 共軛混合積4.2.4 標準平面...
3.3 波束形成的最佳權矢量 3.4 空間譜估計中的線性預測算法 3.5 線性預測算法...9.3 空間譜估計中的循環平穩算法 9.4 空間譜估計中的共軛循環平穩算法 9.5 ...
L空間都是巴拿赫空間,但只有當p= 2的時候,L空間是希爾伯特空間。也就是說,可以為L空間中的元素定義內積。具體形式是:其中的 表示複數的共軛。這個內積是從2-...
固體物理學專業術語。和布拉格矢量(晶格矢量)共軛的另一組矢量基,俗稱動量-能量空間,適合於用來描述聲子電子的晶格動量。...
在量子力學裡,一個量子系統的量子態可以抽象地用態向量來表示。態矢量存在於內積空間。定義內積空間為增添了一個額外的內積結構的矢量空間。態矢量滿足矢量空間所有...
對偶向量族(dual family of vectors)是分別來自賦范線性空間與其共軛空間的滿足一定條件的一對子集。...
