共線方程

共線方程是表達物點、像點和投影中心（對像片而言通常是鏡頭中心）三點位於一條直線的數學關係式，是攝影測量學中最基本的公式之一。

基本介紹

• 中文名：共線方程
• 外文名：Collinearity Equation
• 全稱：共線條件方程
• 所屬學科：攝影測量學

方程

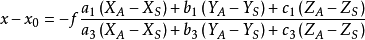
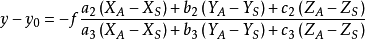
式中：

• x，y 為像點的像平面坐標；
  
• x₀，y₀，f 為影像的內方位元素；
  
• X_S，Y_S，Z_S 為攝站點的物方空間坐標；
  
• X_A，Y_A，Z_A 為物方點的物方空間坐標；
  
• a_i，b_i，c_i （i = 1,2,3）為影像的 3 個外方位角元素組成的 9 個方向餘弦。
  

推導

圖1-推導共線方程

如圖1所示，S 為攝影中心，在某一規定的物方空間坐標中其坐標為（X_S，Y_S，Z_S），A 為任一物方空間點，它的物方空間坐標（X_A，Y_A，Z_A）。a 為 A 在影像上的構像，相應的像空間坐標和像空間輔助坐標分別為（x，y，-f）和（X，Y，Z）。攝影時 S、A、a三點位於一條直線上，那么像點的像空間輔助坐標與物方點物方空間坐標之間有以下關係：

則 ①

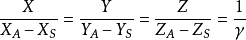
像空間坐標與像空間輔助坐標有下列關係：

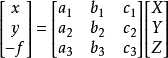
將上式展開為

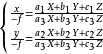
將①式帶入上式得到共線方程。

方向餘弦

像點空間直角坐標的旋轉變換是指像空間坐標與像空間輔助坐標之間的轉換。由高等數學知道，空間直角坐標的變換是正交變換，一個坐標系按某種順序依次旋轉三個角度即可變換為另一個同原點的坐標系。

設像點 a 在像空間坐標系中的坐標（x，y，-f），而在像空間輔助坐標系中的坐標為（X，Y，Z），兩者之間的正交變換關係可以用下式表示：

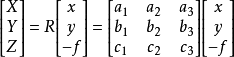
或

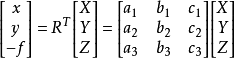
式中 R為3X3階的正交矩陣，它由9個方向餘弦所組成。

由正交矩陣 RR^T=I 的特點，可導出旋轉矩陣中9個方向餘弦之間有下列關係：

1. 同一行（列）的各元素平方和為1；
   
2. 任意兩行（列）的對應元素乘積之和為0；
   
3. 旋轉矩陣的行列式 |R|=1；
   
4. 每個元素的值等於其代數餘子式；
   
5. 每個元素的值為變換前後兩坐標軸相應的夾角的餘弦（如下表）。
   

變換前後兩坐標軸相應的夾角的餘弦

cos	x	y	z
X	a1	a2	a3
Y	b1	b2	b3
Z	c1	c2	c3

以影像外方位元素ψ，ω，κ 系統為例，對於上述兩種坐標系之間的轉換關係可以這樣理解，即像空間坐標系是像空間輔助坐標系（相當於攝影光束的起始位置）依次繞相應的坐標軸旋轉ψ，ω，κ三個角度以後的位置。此時旋轉矩陣 R 可表示為：

由上式可以看出，如果已知一幅影像的3個姿態角元素ψ，ω，κ ，就可以求出9個方向餘弦，也就知道像空間坐標系轉換到像空間輔助坐標系的正交矩陣R，從而可以實現兩坐標的相互轉換。

反演公式

共線方程的另一種形式（反演公式）：

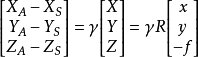
則有

套用

共線方程的主要套用有：

1. 單像空間後方交會和多像空間前方交會；
   
2. 解析空中三角測量光束法平差中的基本數學模型；
   
3. 構成數字投影的基礎；
   
4. 計算模擬影像數據（已知影像內外方位元素和物點坐標求像點坐標）；
   
5. 利用數字高程模型（DEM）與共線方程製作正射影像；
   
6. 利用 DEM 與共線方程進行單幅影像測圖。