空間後方交會,是指利用航攝像片上三個以上不在一條直線上的控制點按共線方程計算該像片外方位元素的方法。是單幅影像解析過程中的一個步驟。
基本介紹
- 中文名:空間後方交會
- 外文名:Space Resection
- 適用學科:攝影測量學
- 套用領域:測繪科學與技術
定義
基本思想
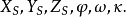
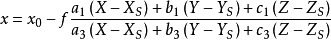
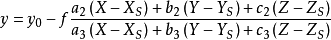
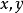
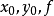
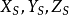
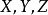
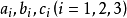

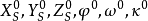
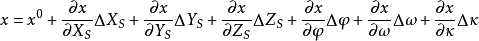

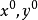
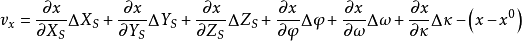

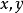
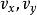
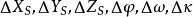

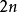
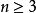
詳細計算
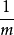
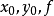
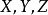
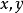
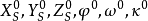
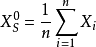
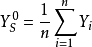
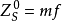
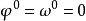
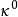
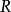
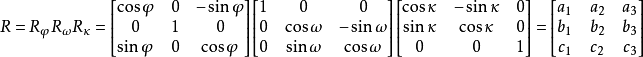
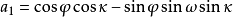
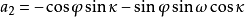
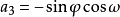
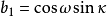

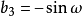
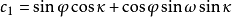
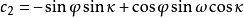
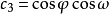
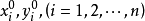
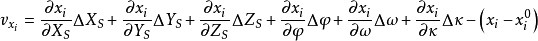
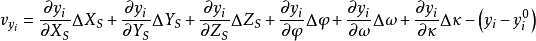
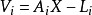
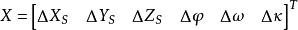
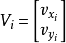
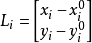
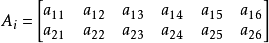
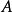
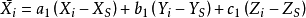
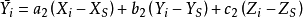
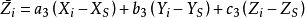
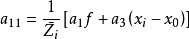

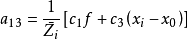
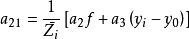
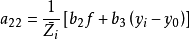
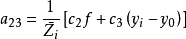
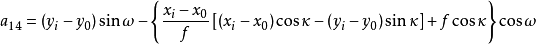
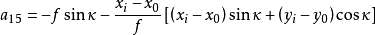

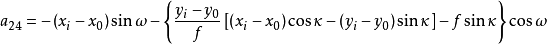
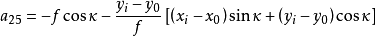
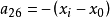
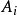
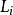
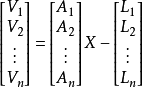
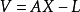
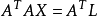

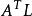
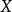
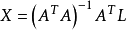
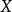
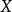
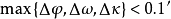
精度評定
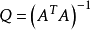
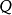

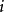
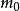
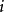
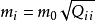

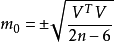
不定性
擴展
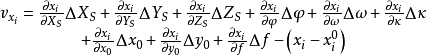
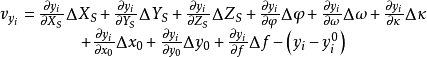
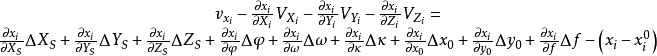
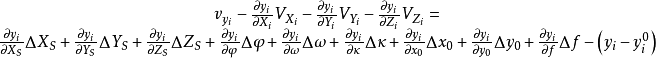
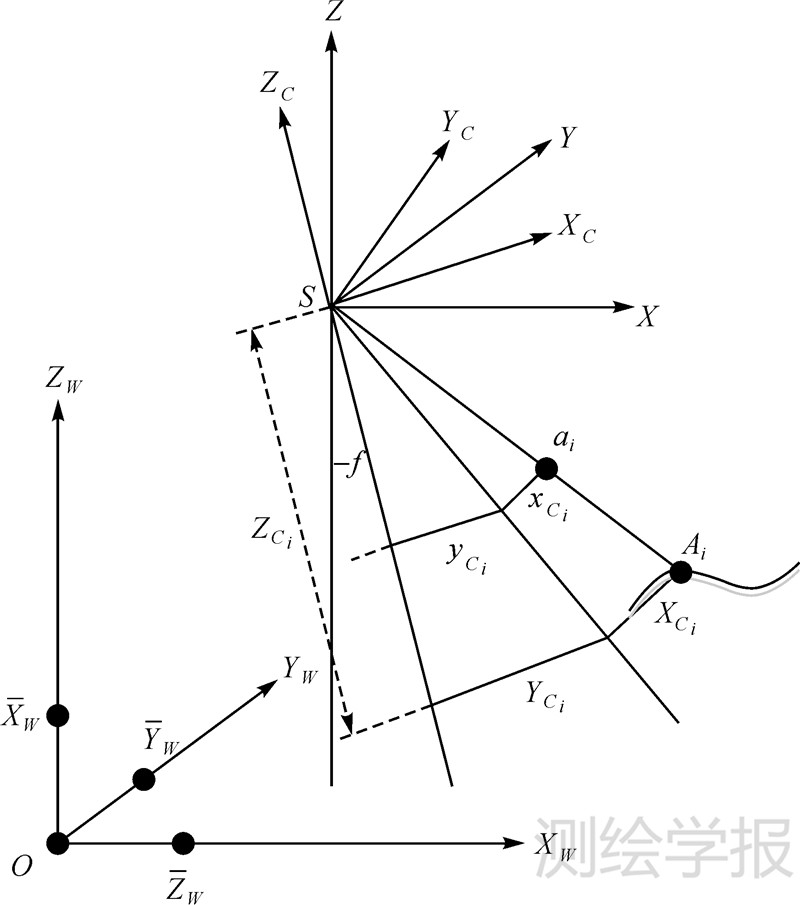
空間後方交會,是指利用航攝像片上三個以上不在一條直線上的控制點按共線方程計算該像片外方位元素的方法。是單幅影像解析過程中的一個步驟。
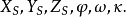
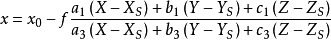
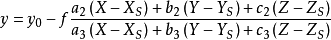
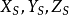
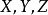
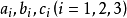

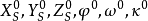
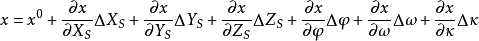

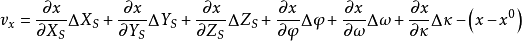

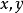
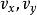
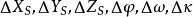

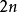
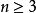
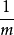
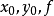
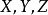
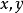
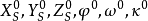
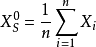
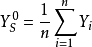
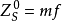
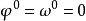
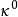
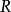
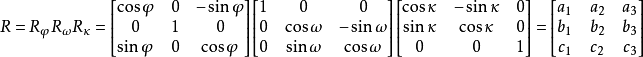
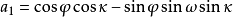
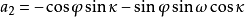
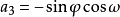
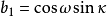

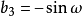
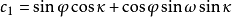
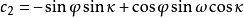
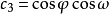
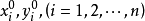
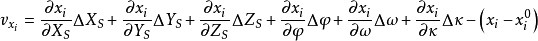
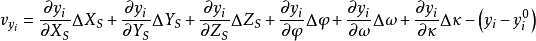
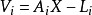
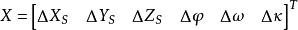
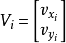
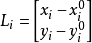
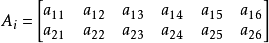
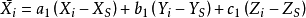
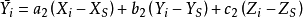
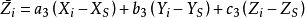
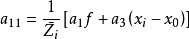

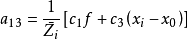
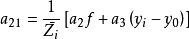
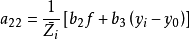
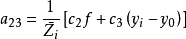
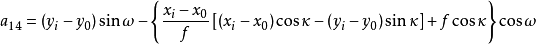
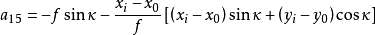

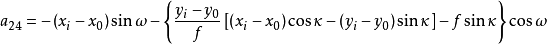
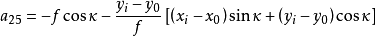
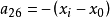
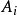
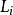
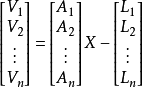
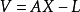
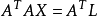

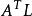
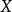
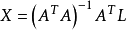
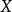
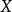
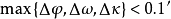
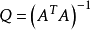
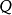

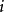
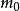
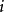
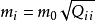

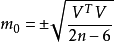
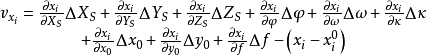
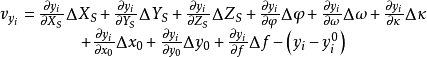
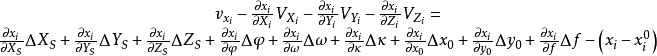
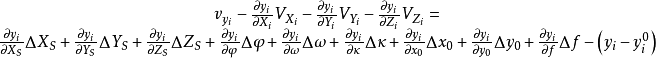
空間後方交會,是指利用航攝像片上三個以上不在一條直線上的控制點按共線方程計算該像片外方位元素的方法。是單幅影像解析過程中的一個步驟。...
單片空間後方交會編輯 鎖定 本詞條缺少信息欄、名片圖,補充相關內容使詞條更完整,還能快速升級,趕緊來編輯吧!1、定義根據影像覆蓋範圍內一定數量的分布合理的地面...
共線方程是中心投影構像的數學基礎,也是各種攝影測量處理方法的重要理論基礎,例如單像空間後方交會、雙像空間前方交會以及光束法區域網平差等一系列問題的原理,都是...
空間後方交會是利用航攝像片上三個以上不在一條直線上的已知點按構像方程計算該像片外方位元素的方法,即由物方已知若干個控制點以及相應像點的坐標,解求攝站的...
1903年他首次利用系留氣球在空中進行攝影,並用投影幾何原理解析地處理空間後方交會,根據3個地面控制點解算空間攝影站點的坐標。他還提出了像片核線的定義和像對的...
1903年他首次利用系留氣球在空中進行攝影,並用投影幾何原理解析地處理空間後方交會,根據3個地面控制點解算空間攝影站點的坐標。他還提出像片核線的定義和像對的相對...
單像空間後方交會和多像空間前方交會; 解析空中三角測量光束法平差中的基本數學模型; 構成數字投影的基礎; 計算模擬影像數據(已知影像內外方位元素和物點坐標求...
第一節 空間坐標系統第二節 攝影的外方位元素第三節 中心投影的構像方程式第四節 旋轉矩陣第五節 微小的轉角第二章單像空間後方交會第一節 概述...
實驗場一般由一些已知空間坐標的標誌點構成,以被檢校的攝影機拍攝此控制場後,可依據單片空間後方交會解法或多片空間後方交會解求內方位元素以及其他影響光束形狀的...
求像點坐標單像空間後方交會和多像空間前方交會攝影測量中的數字投影基礎航空影像模擬光束法平差的基本數學模型利用DEM製作數字正射影像圖利用DEM進行單張像片測圖...
官雲蘭,程效軍,周世健,廖中平,魯鐵定.基於單位四元數的空間後方交會解算.測繪學報,2008.No.1.官雲蘭,周世健,張明,魯鐵定.三維雷射掃描數據配準方法.工程勘察.2008...
空間後方交會是利用航攝像片上三個以上不在一條直線上的已知點按構像方程計算該像片外方位元素的方法,即由物方已知若干個控制點以及相應像點的坐標,解求攝站的...
1. 非量測數位相機單像空間後方交會的輔助分步像主距與像主點的簡單測定 .中國知網.2009-03-20[引用日期2017-09-21] 2. 航測成圖主要環節的技術探討 .中國...
主要包括航攝像片的內定向、像片坐標量測、空間後方交會及前方交會、相對定向及絕對定向、航帶法空中三角測量、光束法空中三角測量、影像立體匹配、影像數字糾正等算法...
5-20 基於平行線相對控制的空間後方交會解法5-21 ATOS系列的三維數位化器第六章 現代工業感測器6-1 位移感測器概述6-2 EX-VOl型感應類位移感測器6-3 LK系列...
官雲蘭、程效軍等,基於單位四元數的空間後方交會解算,測繪學報(EI檢索),2008,vol.37(1):30-356.官雲蘭、程效軍等,一種穩健的點雲數據平面擬合方法,同濟大學...
像片主距是數字投影的基礎,它作為影像的內方位元素之一,可用於各種攝影測量處理問題,包括基於共線方程的單像空間後方交會、雙像空間前方交會以及光束法區域網平差等...
水下攝影測量技術就是利用物方空間在水中、像方空間在空氣中所拍攝的圖像,確定...首先通過空間後方交會,疊代解算出準確的各攝站的外方位元素;然後再通過空間前方...
43 兩種單像空間後方交會模型分析 光學技術 2010-01-1544 一種機載雙天線InSAR干涉參數定標新方法 測繪學報 2010-02-1545 一種基於正弦模型的干涉SAR射頻干擾...
19. 基於角錐體原理的空間後方交會改進算法, 2006.2, , 測繪科學。20. “3S”技術在內蒙古牧業上的套用, 2006.2, , 內蒙古農業科技。...
然後直接用航帶法求出各地而點坐標進行空間後方交會,求出所需像片的外方位元素。把這些值作為光束法平差計算的初始值 [1] 。獨立模型法空中三角測量區域網平差...
8.1.2空間後方交會及前方交會解算 8.1.3數碼影像空間後交的精度分析 8.1.4多片前交的精度及可靠性 8.2數碼影像的相對定向 8.2.1相對定向疊代解法...
任務2.3中心投影構像方程及單張像片空間後方交會 15 任務2.4攝影測量常用坐標系統及圖形分幅要求 17 任務2.5數字攝影測量的數據分析與準備 24 任務2.6數字航空影像...
坐標量測裝置可量測承影面上控制點的坐標,計算機按空間後方交會原理計算出各種變換參數,並藉助於攝影機主距和糾正儀物鏡焦距、以及糾正係數(攝影比例尺分母與糾正...
