基本介紹
- 中文名：全等圖形
- 外文名：Congruent figures
- 拼音：Quán děng tú xíng
- 學科：數學
- 概念：能夠完全重合的兩個圖形
- 簡稱：全等形
基本內容,比較,全等三角形,相關例題,教學套用,
基本內容
一個圖形經過平移、翻折、旋轉後，位置變化了，但形狀和大小都沒有改變，即平移、翻折、旋轉前後的圖形全等。即一個圖形經過平移、旋轉或翻折等變換後，所得到的新圖形一定與原圖形全等。反過來，兩個全等的圖形經過平移、旋轉或翻折變換後一定可以重合。
比較
相似圖形：形狀相同的平面圖形。特點是形狀形同，大小不一定相同。
全等圖形：能夠完全重合的平面圖形。特點是形狀、大小相同。
兩者的關係：兩個相似圖形未必是全等圖形；兩個全等圖形一定是相似圖形。全等圖形是特殊的相似圖形。例如，全等三角形是相似三角形當相似比等於1時的特例，因而全等圖形與相似圖形之間體現了從特殊到一般關係的推廣。
全等三角形
全等圖形在數學中被廣泛套用。其中套用較多的是全等三角形。全等三角形是指能夠完全重合的三角形。
全等三角形的性質：
1.全等三角形對應邊相等；
2.全等三角形對應角相等。
判定公理：
2.兩邊和它們的夾角對應相等的兩個三角形全等(簡稱SAS或“邊角邊”)；
3.兩角和它們的夾邊對應相等的兩個三角形全等(簡稱ASA或“角邊角”)；
4.兩個角和其中一個角的對邊對應相等的兩個三角形全等(簡稱AAS或“角角邊”)；
在三角形全等的判定中，沒有AAA(角角角)和SSA(邊邊角)，其中A是英文角的縮寫(angle)，S是英文邊的縮寫(side)。H是英文斜邊的縮寫（hypotenuse），L是英文直角邊的縮寫（leg）。
相關例題
例1.幾何中，我們把“一模一樣”的圖形叫做全等圖形，以下是描述全等圖形的三種不同的說法，你認為哪種說法是恰當的？
（1）形狀相同的兩個圖形；
（2）大小相等的兩個圖形；
（3）能夠完全重合的兩個圖形。
解：全等形要滿足兩個基本條件，兩個圖形的形狀完全相同和大小完全相同，所以（3）正確。
例2.如圖1所示，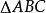
與
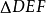為全等三角形，AB=4，求DE長度。
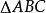
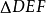
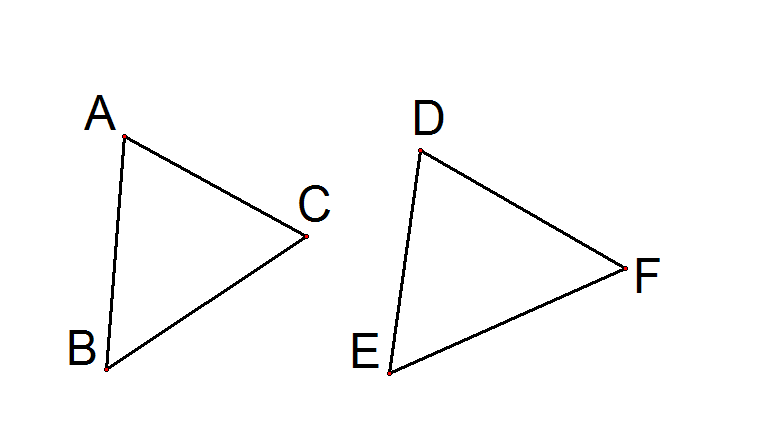圖1解：由全等圖形的性質可知AB=DE=4。
教學套用
在全等圖形的數學教學中可以採用“探究法”。“探究法”的精髓在於以學生為主角，使他們由被動地接受知識轉變為知識的探索者。通過親自動手，積極思考，熱烈討論，探索知識，學生能更加深入理解知識的內涵，並培養觀察力、思維能力、動手能力、歸納能力、語言表達能力和創造能力等。“探究式教學法 ”是指在老師的指導下 ，學生通過具體的操作，親自嘗試後，經過積極思考和討論，找到知識的規律，總結出結論，學會新知，並發展思維、培養能力的綜合教學方法。通過讓學生對全等和相似進行區分，可以引導學生對全等圖形與相似圖形之間的關係進行積極思考，明確兩個相似圖形未必是全等圖形，兩個全等圖形一定是相似圖形的結論，從而使學生更加深入掌握全等圖形這一知識點，從中拓展學生思維、提高學生獨立思考的能力。
