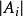克萊姆組

秩為n的含n個未知數的n個線性方程的方程組稱為克萊姆組。這樣的方程組有唯一解，我們可以藉助於行列式除法將它表示出來(克萊姆公式)。

基本介紹

• 中文名：克萊姆組
• 所屬學科：數學
• 相關概念：線性方程組，克萊姆公式等
• 要點：秩為n含n個未知數的n個線性方程

基本介紹

克萊姆組是指秩為n的含n個未知數的n個線性方程的方程組。這樣的方程組有唯一解，我們可以藉助於行列式除法將它表示出來(克萊姆公式)。例如，方程組

若且唯若 時，是克萊姆方程組，在這種情況下，克萊姆公式可寫成

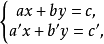
除這種情況以外，克菜姆公式雖有理論上的價值，但對數值套用來說並不好用，較為常用的有高斯主元法，或建立在矩陣分解基礎上的類似方法，像在數值方程情況中那樣，也可用逐次逼近法。

相關知識

線性方程組

把

叫做含m個未知元n個方程的線性方程組， 是線性方程組中已知的元素，未知量 是線性方程組中需要尋求的元素，滿足這個方程組的任何序列( )叫做一個解， 叫做右邊，若 ，方程組叫做齊次方程組，齊次方程組至少有一個稱為零解的解 。對於任意的 ，將右邊用0代替後所得的新方程組叫做與原方程組相伴的齊次方程組。

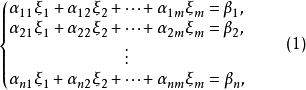
克萊姆組

定理 假定 就是說方程個數和未知量個數一樣多時，下列條件便彼此成立：

（i）矩陣 可逆；

（ii）不論右邊為何，方程組（1）至少有一解；

（iii）不論右邊為何，方程組（1）至多有一解；

（iv）不論右邊為何，方程組（1）有而且只有一解；

（v） ；

（vi）相伴齊次方程組只有零解。

定義 若 ，方程組（1）便叫做克萊姆組。

克萊姆公式

讓我們首先來考察含兩個變數兩個線性方程的方程組，它的一般形式為

用代數加法求解它。為此將第1個方程乘以 ，將第2個方程乘以 ，然後將它們相加；再將第1個方程乘以 ，第2個方程乘以 ，同樣將它們相加。如果 ，則得公式

式(3)中的分母是相同的，且不難看出， ，即它是方程組(2)的係數行列式。

式(3)中的分子同樣可表示為行列式

容易看出，行列式 是以自由項替換行列式 中變數 的係數而得到的，行列式 是以自由項替換行列式 中變數 的係數而得到的，因此式(3)可寫成

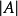
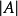
因而，如果方程組(2)的行列式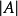異於零，則方程組是相容的，而它的解可由式(5)求出，式(5)稱為克萊姆公式。

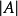
定理 如果含有n個變數n個線性方程的方程組的係數行列式不等於零，則這個方程組是確定的，它的唯一解可按下列公式求出： ·

式中 是在方程組的係數行列式 中以自由項替換變數 的係數而得到的行列式。