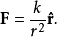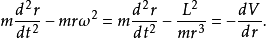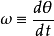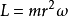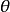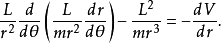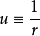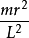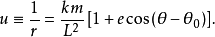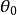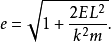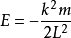克卜勒問題

克卜勒問題

在經典力學里，克卜勒問題是二體問題的一個特別案例。假若，兩個物體以有心力互相作用；力的大小與距離的平方成反比。則稱此物理系統所涉及的問題為克卜勒問題。

基本介紹

背景,定義,問題解析,相關術語,

背景

克卜勒問題是因天文學家約翰內斯·克卜勒而命名。他推出了在天文學歷史上，具有關鍵價值的克卜勒定律。遵守克卜勒定律的作用力有哪些特性呢（逆克卜勒問題）？在這方面，他也做了很多的研究。
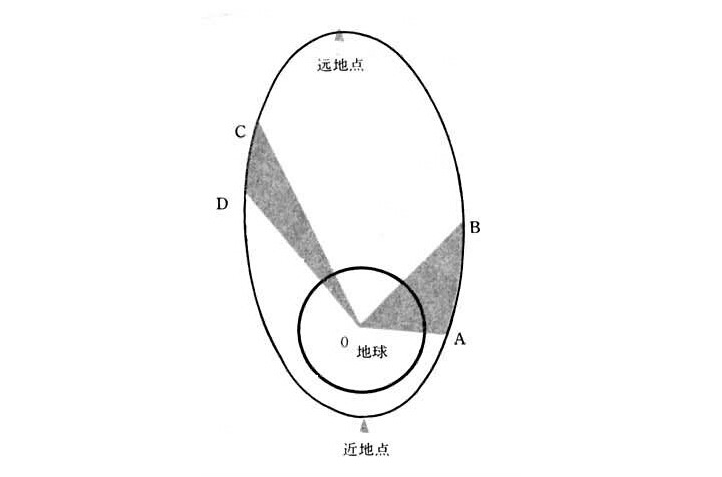
在很多狀況下，會遇到克卜勒問題。天體力學時常會涉及克卜勒問題，因為牛頓萬有引力遵守反平方定律。例如，人造衛星環繞著地球，行星環繞著太陽，或雙星系統。克卜勒問題涉及了兩個電荷子的物理運動，因為靜電學的庫侖定律遵守反平方定律。例如，氫原子，正子素，與μ子偶素。這些典型系統，在測驗物理理論與測量自然常數上，都扮演了很重要的角色。
在經典力學裡，克卜勒問題與諧振子問題是兩個最基本的問題。只有這兩個問題的解答是閉合軌道；也就是說，物體從一點移動，經過一段路徑後，又回到原先點。在經典力學里，克卜勒問題時常被用來發展新的表述方法，像拉格朗日力學，哈密頓力學，哈密頓-亞可比方程，與作用量-角度坐標。在克卜勒問題里，拉普拉斯-龍格-楞次矢量是一個運動常數。克卜勒問題的解答使科學家能夠用經典力學完全地解釋清楚行星運動。這行星運動的科學解釋在啟蒙時代的開啟扮演了重要的角色。

定義

在經典力學里，克卜勒問題是二體問題的一個特別案例。假若，兩個物體以有心力F互相作用；力的大小與距離r的平方成反比。則稱此物理系統所涉及的問題為克卜勒問題。反平方有心力以公式表示為
其中，k是常數，
是徑向單位矢量。
有心力可以是吸引性的（k<0），也可以是排斥性的（k>0），對應的位勢為

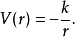
問題解析

所有的吸引性的有心力都能夠形成圓形軌道，前提是有心力必須相等於粒子的向心力。給定圓半徑，這要求相當於物體的角速度已被決定。在此條目里，不會提到非有心力。一般而言，非有心力不能形成圓形軌道。
假設，一個質量為m的粒子移動於一個連心勢V(r)內。r是徑向坐標。其拉格朗日方程為
其中，時間是t，角速度是
，運動常數角動量是
。
詳細說明，對於圓形軌道，方程左手邊第一項目等於零；如預期，有心力
相等於向心力。角動量定義可以將自變數從t改變為
：
這樣，新的運動方程不含時間：
變數變換
，將方程兩邊乘以
，則可得二次微分方程：
對於一個反平方作用力，像萬有引力或靜電力，位勢可以表示為
代入微分方程，
導引出軌道為
其中，離心率是e，相位常數是
。這些都是積分常數。
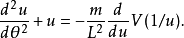
這是一個焦點在力中心點的圓錐曲線方程。圓錐曲線的離心率與總能量E有關：
假若
，則e=0，軌道是圓形的；假若E<0，則e<1，軌道是橢圓形的；假若E=0，則e=1，軌道是拋物線；假若 E>0，則e>1，軌道是雙曲線。

相關術語

相關詞條

熱門詞條

聯絡我們