基本介紹
- 中文名:自然常數
- 外文名:e
- 本質:一個無限不循環數,超越數
- 大小:約為2.718281828
起源,收斂性證明,另外形式,計算方法,套用,
起源
e,作為數學常數,是自然對數函式的底數。有時稱它為歐拉數(Euler number),以瑞士數學家歐拉命名;也有個較鮮見的名字納皮爾常數,以紀念蘇格蘭數學家約翰·納皮爾 (John Napier)引進對數。它就像圓周率π和虛數單位i,e是數學中最重要的常數之一。
它的其中一個定義是 ,其數值約為(小數點後100位):“e ≈ 2.71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 95749 66967 62772 40766 30353 54759 45713 82178 52516 64274”。
,其數值約為(小數點後100位):“e ≈ 2.71828 18284 59045 23536 02874 71352 66249 77572 47093 69995 95749 66967 62772 40766 30353 54759 45713 82178 52516 64274”。

第一次提到常數e,是約翰·納皮爾(John Napier)於1618年出版的對數著作附錄中的一張表。但它沒有記錄這常數,只有由它為底計算出的一張自然對數列表,通常認為是由威廉·奧特雷德(William Oughtred)製作。第一次把e看為常數的是雅各·伯努利(Jacob Bernoulli)。
已知的第一次用到常數e,是萊布尼茨於1690年和1691年給惠更斯的通信,以b表示。1727年歐拉開始用e來表示這常數;而e第一次在出版物用到,是1736年歐拉的《力學》(Mechanica)。雖然以後也有研究者用字母c表示,但e較常用,終於成為標準。
用e表示的確實原因不明,但可能因為e是“指數”(exponential)一字的首字母。另一看法則稱a,b,c和d有其他經常用途,而e是第一個可用字母。不過,歐拉選這個字母的原因,不太可能是因為這是他自己名字Euler的首字母,因為他是個很謙虛的人,總是恰當地肯定他人的工作。
以e為底的指數函式的重要方面在於它的函式與其導數相等。e是無理數和超越數(見林德曼—魏爾施特拉斯定理(Lindemann-Weierstrass))。這是第一個獲證的超越數,而非故意構造的(比較劉維爾數);由夏爾·埃爾米特(Charles Hermite)於1873年證明。
其實,
融合e,π的的歐拉公式 ,也是超越數e的數學價值的最高體現。
,也是超越數e的數學價值的最高體現。

自然常數一般為公式中乘方的底數和對數的底。為什麼會這樣,主要取決於它的來歷。
自然常數的來法比圓周率簡單多了。它就是當 時函式
時函式 值的極限。
值的極限。


即: 。
。

同時,它也等於 。注意,
。注意, 。
。


因為e=2.7182818284... ,極為接近循環小數2.71828(1828循環),那就把循環小數化為分數271801/99990,所以可以用271801/99990表示為e最接近的有理數約率,精確度高達99.9999999(7個9)% 。
收斂性證明
由均值不等式,有

即序列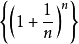 單調上升;另一方面,我們嘗試證明
單調上升;另一方面,我們嘗試證明 。即要證
。即要證 ,由均值不等式得
,由均值不等式得
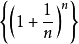



又明顯有 ,故
,故 成立,所以
成立,所以 成立。
成立。



故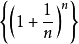 單調上升有上界,即
單調上升有上界,即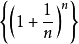 收斂。
收斂。
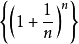
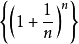
另外形式

證法1
令 ,易知
,易知


則已知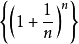 收斂於
收斂於 ,即
,即
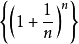


即

所以, ,不妨設
,不妨設 ,則有
,則有



即 ,有
,有



又易知對固定的 和
和 ,有
,有







即 ,當 時,有
,當 時,有 ,即
,即



即

註:由該證法可以看出,對任意正數序列 ,若存在一個收斂數列
,若存在一個收斂數列 ,使得
,使得



則 收斂,且極限為
收斂,且極限為 .
.


證法2
欲證 ,即要證
,即要證



則有

故有

證畢.
計算方法
泰勒公式展開

取Peano形式的餘項

令上式 ,有
,有


故有

即得
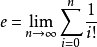
由此就可根據上式求解出 的具體數值
的具體數值

限制精度
但是在套用中我們需要的是 的具有某位精度的數值,比如說要求
的具有某位精度的數值,比如說要求 的小數點前2000位的準確數值。此時Peano餘項不夠用了。我們換一個餘項,例如——Lagrange餘項:
的小數點前2000位的準確數值。此時Peano餘項不夠用了。我們換一個餘項,例如——Lagrange餘項:







所以





便得 的小數點後t位的準確數值
的小數點後t位的準確數值

套用
自然常數e在科學上有廣泛套用。以下舉幾例:
1:e對於自然數的特殊意義
所有大於2的2n形式的偶數存在以 為中心的共軛奇數組,每一組的和均為2n,而且至少存在一組是共軛素數
為中心的共軛奇數組,每一組的和均為2n,而且至少存在一組是共軛素數

可以說 是素數的中心軸,
是素數的中心軸, 只是奇數的中心軸。
只是奇數的中心軸。


2:素數定理
自然常數也和質數分布有關。有某個自然數a,則比它小的質數就大約有 個。在a較小時,結果不太正確。但是隨著a的增大,這個定理會越來越精確。這個定理叫素數定理,由高斯發現。
個。在a較小時,結果不太正確。但是隨著a的增大,這個定理會越來越精確。這個定理叫素數定理,由高斯發現。

3:完全率
設完全圖 內的路徑總數為W,哈密頓路總數為h,則W/h=e,此規律更證明了e並非故意構造的,e甚至也可以稱呼為是一個完全率。與圓周率有一定的相類似性,好像極限完全圖就是圖論中的圓形,哈密頓路就是直徑似的,自然常數的含義是極限完全圖裡的路徑總數和哈密頓路總數之比。
內的路徑總數為W,哈密頓路總數為h,則W/h=e,此規律更證明了e並非故意構造的,e甚至也可以稱呼為是一個完全率。與圓周率有一定的相類似性,好像極限完全圖就是圖論中的圓形,哈密頓路就是直徑似的,自然常數的含義是極限完全圖裡的路徑總數和哈密頓路總數之比。

4:雙曲函式
雙曲函式是自然常數價值的重要體現。它可以解決很多問題。如:
阻力落體
解:
小石塊遵循的運動方程為
mdv/dt=mg―μv2
(1)
這是Riccati方程,它可以精確求解。
依標準變換方式,設
v=(m/μ)/(z′/z) (2)
代入(1)式,再作化簡,有
z'' ―(gμ /m)z=0 (3)
(3)式的通解是
z=C1exp(√gμ /m t)+ C2exp(-√gμ /m t)(4)
其中,C1和C2是任意常數。
由於小石塊在初始時刻是靜止的,初始條件為
v(0)=0 (5)
這等價於
z′(0)=0 (6)
因此,容易定出
C2=C1 (7)
將(7)式代入(4)式,再將(4)式代入(2)式,就可得
滿足初始條件的解
v=√mg/μ tanh(√μg/m t) (8)
我們可以作一下定性的分析。小石塊初始時刻靜止。因此,隨著時間增加,開始時小石塊速度較小,小石塊所受的阻力影響較小,此時,小石塊與不受阻力的自由落體運動情況相類似,小石塊加速度幾乎是常數。反映在圖1中,起始段t和v的關係是直線。當小石塊速度很大時,重力相對於阻力來說可以忽略,阻力快速增加到很大的數值,導致小石塊的速度幾乎不再增加。此時,小石塊加速度接近零,v幾乎不隨時間而變化。一段時間後,v相不多是一平行於t軸的直線。
粒子運動
一電荷量為q、靜質量為m0的粒子從原點出發,在一均勻電場E中運動,E=Eez沿z軸方向,粒子的初速度沿y軸方向,試證明此粒子的軌跡為[4]
x=(W0/qE)[cosh(qEy/p0c)―1] (1)
式中p0是粒子出發時動量的值,W0是它出發時的能量。
解:
帶有電荷量q的粒子在電磁場E和B中的相對論性的運動方程為
dp/dt=q(E+v×B) (2)
式中v是粒子的速度,p是粒子的動量
p=mv=mv0/√1-v2/c2 (3)
本題運動方程的分量表示式為
dpx=qE
dpy=0
dpz=0 (4)
解之,有
px =qEt+C1
py = C2
pz = C3 (5)
代入t=0時初始條件
px(0)=0
py(0)= p0
pz(0)= 0 (6)
定出積分常數後,可知
px=qEt
py= p0
pz= 0 (7)
W=mc2
=√p2c2+m02c4
=√(px2+ py2+ pz2)c2+m02c4
=√q2E2 c2t2+W02 (8)
因dx/dt=qEt/m=qEc2t/√q2E2 c2t2+W02 (9)
積分得
x=∫[qEc2t/√q2E2 c2t2+W02 ]dt
= [√q2E2 c2t2+W02 -W02]/qE (10)
又由(7)式得
dy/dt=p0/m=p0c2/√q2E2 c2t2+W02 (11)
積分得
y=∫[p0c2 /√q2E2 c2t2+W02 ]dt
=(p0c /qE)arsh(qEct/W0) (12)
或 (qEct/W0)= sinh (qEy/ p0c) (13)
在(51)式和(54)式中消去t,有
x=(W0/qE)[√1+ sinh2(qEy/ p0c)-1 ] (14)
利用恆等變換公式
cosh2x―sinh2x=1 (15)
(55)式可以寫成
x=(W0/qE)[cosh2(qEy/ p0c)-1 ] (16)
(16)式是一種懸鏈線。
討論:
因雙曲餘弦泰勒級數展開式是
cosh(x)=1+x2/2!+x4/4!+x6/6!+…… (17)
當v/c →0時,保留前2項,得
x=(qE/2m v02)y2 (18)






