信源編碼是一種以提高通信有效性為目的而對信源符號進行的變換,或者說為了減少或消除信源冗餘度而進行的信源符號變換。具體說,就是針對信源輸出符號序列的統計特性來尋找某種方法,把信源輸出符號序列變換為最短的碼字序列,使後者的各碼元所載荷的平均信息量最大,同時又能保證無失真地恢復原來的符號序列。
基本介紹
編碼結果
作用
方式
定理
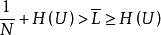
分類
套用
 表1 信源編碼實例表
表1 信源編碼實例表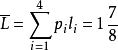
通信系統模型
專業表述
 信源編碼
信源編碼 信源編碼
信源編碼 信源編碼
信源編碼 信源編碼
信源編碼信源編碼是一種以提高通信有效性為目的而對信源符號進行的變換,或者說為了減少或消除信源冗餘度而進行的信源符號變換。具體說,就是針對信源輸出符號序列的統計特性來尋找某種方法,把信源輸出符號序列變換為最短的碼字序列,使後者的各碼元所載荷的平均信息量最大,同時又能保證無失真地恢復原來的符號序列。
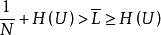
 表1 信源編碼實例表
表1 信源編碼實例表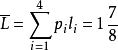
 信源編碼
信源編碼 信源編碼
信源編碼 信源編碼
信源編碼 信源編碼
信源編碼信源編碼是一種以提高通信有效性為目的而對信源符號進行的變換,或者說為了減少或消除信源冗餘度而進行的信源符號變換。具體說,就是針對信源輸出符號序列的統計...
在資訊理論中,香農的信源編碼定理(或無噪聲編碼定理)確立了數據壓縮的限度,以及香農熵的操作意義。信源編碼定理表明(在極限情況下,隨著獨立同分布隨機變數數據流的...
將訊息或其特徵信號經採樣變換為數字代碼的技術。訊息(信源信號)一般為連續變化的模擬量,若直接用這連續變化的信號進行調製、傳輸,則稱為模擬通信;若經編碼變為...
AVS是我國具備自主智慧財產權的第二代信源編碼標準,是《信息技術 先進音視頻編碼》系列標準的簡稱,其包括系統、視頻、音頻、數字著作權管理等四個主要技術標準和符合性...
多用戶信源編碼:是指研究多個相關信源的編碼的主要目的是壓縮信息率。若兩個離散信源各發出符號U1和U2,它們的信息熵分別是H(U1)和H(U2),條件熵(以U1為條件...
信源解碼是指將數位訊號轉換為模擬信號的方法,與信源編碼對應。...... 信源編碼是一種以提高通信有效性為目的而對信源符號進行的變換,或者說為了減少或消除信源...
《信源編碼原理與套用》是北京郵電大學出版社2015-12出版的信息與通信或相關專業的研究生教材,作者為田寶玉、賀志強、楊潔、許文俊。...
變長信源編碼定理(source coding theorem ofvariable length)信源編碼理論的基本定理之一對於由n個字母構成的字母表A = {a},az,"..}a ),編碼由m個訊息構成...
通用編碼是對於統計特性未知的信源所進行的有效編碼。一類以估計信源的機率統計特性為基礎;另一類以序列複雜度理論為基礎。...
《資訊理論與信源編碼理論及套用》是2010年4月1日出版的圖書,作者劉建成。本書試圖以知識性、研究性、實用性、先進性、綜合性的內容為主線,給讀者介紹信息理論和...
《數位電視信源編碼技術與套用》是2012年出版的圖書,作者是熊紅凱。...... 《數位電視信源編碼技術與套用》圍繞視頻編碼國際標準,系統介紹了信源編碼技術的基本原理...
信源是產生各類信息的實體。信源給出的符號是不確定的,可用隨機變數及其統計特性描述。信息是抽象的,信源則是具體的。例如,人們交談,人的發聲系統就是語聲信源;...
如果需承載更高碼率的IPTV 節目,每個用戶的接入頻寬有限,而且在大規模用戶的情況下,也沒有足夠高輸出頻寬的伺服器,因此視頻壓縮編碼的壓縮比應該儘量高。視頻編碼...
信源編碼定理(申農第一定理)給出了解決前一個問題的可能性,並同時給出了一種編碼方法;有噪信道編碼定理(申農第二定理)指出存在著這樣的編碼,它可使傳輸的錯誤...
等長信源編碼定理(source coding theorem offixed-length)信源編碼理論的基本定理之一,是指一個熵為H (S)的離散無記憶信源,若對信源長為N的符號序列進行等長...
《資訊理論與編碼技術(電子信息)》系統地講述了資訊理論及編碼的基礎理論,共分為6章,即緒論、信息及其度量、信道及其容量、信源編碼、信道編碼和保密通信。《資訊理論與...
在資訊理論中,香農的信源編碼定理(或無噪聲編碼定理)確立了數據壓縮的限度,以及香農熵的操作意義。信源編碼定理表明(在極限情況下,隨著獨立同分布隨機變數數據流的...
聯合信源信道編碼是英文文獻中翻譯: Joint source-channel coding(JSCC)。...... 聯合信源信道編碼是英文文獻中翻譯: Joint source-channel coding(JSCC)。...
香農(Shannon)編碼是一種常見的可變字長編碼,與哈夫曼編碼相似,當信源符號出現的機率正好為2的負冪次方時,採用香農-范諾編碼同樣能夠達到100%的編碼效率。香農編碼...
《資訊理論與編碼原理》系統地講述了資訊理論與編碼的基本理論,共11章,內容包括:信息的基本概念、信源及其信息量、信道及其容量、信息率失真函式、信源編碼和信道編碼...
H.261定義的編解碼器由信源編碼器、視頻複合編碼器、傳輸緩 視頻編解碼器框圖 沖器、傳輸編碼器以及編碼控制部分組成。整個編碼過程的核心仍在信源編碼部分。編...
一般來說,任何一種能把書面字元用可變長度的信號表示的編碼方式都可以稱為摩爾斯...電報公司根據要發的信的長度收費。商業代碼精心設計了五個字元組成一組的代碼,做...
