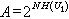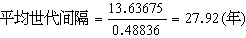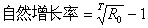基本簡介
當U1和U2兩個信源不在同一地方,而U1的樣已為信宿所確知,但對U2編碼時卻不確知U1當時的樣,那么只要信息率大於H(U2│U1),就能把U2編碼後傳送給信宿,而使後者能正確譯出U2。這就是具有邊信息的多用戶信源編碼定理。信宿已確知的U1就稱為對U2解碼的邊信息。這可由容量大於H(U1)的信道傳送。
原理過程
要證明關於離散無記憶信源的這一定理,可以用典型序列的概念(見
漸近等分性)。當信源符號數目
N足夠大時,
U1組成的典型序列有個,對應每個
U1序列,
U2組成的典型序列有個,這些序列可排成
A行
B列的矩陣。對
U2編碼時只須把這個序列在矩陣的列號編成碼,於是所需的信息率就是
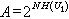
在解碼時,因已知
U1序列的樣,即已知在哪一行,就可根據列號從矩陣中找出被傳送的那一個
U2序列。因此只要
U2是典型序列,便可以無錯誤地解碼。已知
N→∞時,非典型序列出現的機率接近於零,因此有邊信息時解碼的差錯機率也接近於零。
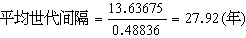
再推廣一步,可研究圖中a的系統。兩個相關信源 U1和U2分別由兩個編碼器編碼後用兩條信道傳送,在接收端同時收到兩條信道的輸出,為了正確譯出1和2,對兩條信道須傳送的信息率R1和R2的要求是R1≥H(U1|U2)
R2≥H(U2|U1)
R1+R2≥H(U1U2)
詳細解釋
這三個不等式所對應的區域是圖中 b所示的陰影部分。利用時分內插編碼原理可以證明,只要(R1,R2)是在圖中的陰影部分內,且符號長度N足夠長,總存在一種編碼方法,使解碼器能正確地譯出U1和U2。因此兩條信道的容量是允許調配的:R1大時,R2可小一些,反之亦然。
另一類多用戶信源問題是利用公用信道和私用信道問題。從兩個相關信源U1和U2引出另一隨機量W,使在W 已知條件下U1和U2相互獨立。此時下列條件機率之間的關係成立P(U1,U2|W )=P1(U1|W )P2(U2|W )
滿足上式的所有W組成一個集E。變更W,使U1和U2作為一組對W 的互信息I(U1U2;W)為最小,此最小值稱為U1和U2之間的共信息I0,即
當利用公用信道傳送
W 時,傳送
U1和
U2的私用信道的信息率
R1和
R2分別只須大於
H(
U1│
W )和
H(
U2│
W )。這種系統的特點是利用私用信道(
R1)傳來的信息和公用信道傳來的
W 就能正確譯出
U1,但很難譯出
U2。因為在
W確知條件下,
U1和
U2是相互獨立的,也就是譯出
U1後對
U2的解譯毫無幫助,這可用於某些保密系統中。另一方面,利用公用信道中的邊信息可降低對私用信道的要求。
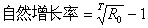
擴展閱讀
多用戶信源編碼是一種尚在發展的理論。對於允許失真的信源問題,也有一些研究結果,其他如有記憶信源以及理論的套用前景等問題,均尚在探索中。