保角對應(conformal correspondence)保持角度不變的一種對應.若在兩個曲面的點之間建立一一對應,使任意兩條曲線的交角在對應下保持不變,則此種對應稱為保角對應,而一個曲面到另一個曲面的映射稱為保角映射,或共形(保形)映射.特別地,將一個曲面到自身的保角映射稱為保角變換.若在兩曲面S和S‘的點之間存在一一對應,且對應點取相同的參數,則該對應為保角對應的充分必要條件是這兩個曲面的第一類基本量成比例,即
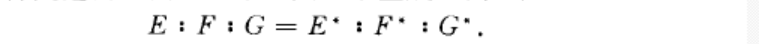
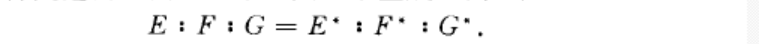
保角映射是複變函數最重要的概念之一,它可以將比較複雜的區域上的問題轉化到比較簡單的區域上進行研究。成功地解決了流體力學、空氣動力學、彈性力學、電學等學科中...
保角對應(conformal correspondence)保持角度不變的一種對應.若在兩個曲面的點之間建立一一對應,使任意兩條曲線的交角在對應下保持不變,則此種對應稱為保角對應,...
保角變換基本知識 編輯 當 變換為單值函式時,對於Z平面上的一個點 ,在W平面就有一點叫 與之對應;對於Z平面上的一條曲線C,W平面就有一條曲線C'與之對應;...
大學數學教程(第2卷第3冊)積分變換、數理方程、保角映射,是大學高等數學學習的一本教程。也可作為數學物理方法課程的補充教材或教學參考書用。...
設C是若爾當區域G的邊界曲線,z=Ψ(w)是將{w|w|>1}映射到C的外部且在∞處規格化的保角映射,f(z)在G內解析,在Ḡ上連續,則稱σn為f(z)的費伯係數...
數學上,共形對稱即共形變換(英語:Conformal map),或稱保角變換,來自於流體力學和幾何學的概念,是一個保持角度不變的映射。...
第28章jacobi保角映射28.1再談圓函式和橢圓函式28.2jacobi橢圓函式的保角映射第29章jacobi濾波器29.1jacobi橢圓函式的雙周期29.2jacobi橢圓函式逼近...
