佩龍下函式

佩龍下函式為定義佩龍積分而引進的概念，與之對應的概念是佩龍上積分。

基本介紹

• 中文名：佩龍下函式
• 外文名：Perron lower function
• 適用範圍：數理科學

簡介

佩龍下函式為定義佩龍積分而引進的概念。

設f(x)是在[a,b]上定義的實值函式（不一定有限），F(x)是在[a,b]上定義的連續函式，為F(x)的上導數。若：

1、F(a)=0；

2、對所有x∈[a,b]，；

3、對所有x∈[a,b]，，則稱F(x)為f(x)的佩龍下函式，簡稱下函式。

佩龍上函式

佩龍上函式為定義佩龍積分而引進的概念。

設f(x)是在[a,b]上定義的實值函式（不一定有限），F(x)是在[a,b]上定義的連續函式，為F(x)的上導數。若：

1、F(a)=0；

2、對所有x∈[a,b]，；

3、對所有x∈[a,b]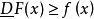，，則稱F(x)為f(x)的佩龍上函式，簡稱上函式。

佩龍積分

佩龍積分是勒貝格積分的推廣，一種非絕對積分。

佩龍(Perron , O.)於1914年在當儒瓦(Denjoy,A.)建立狹義當儒瓦積分後，定義的另一類型的積分；

哈克(Hake , H.)於1921年證明了狹義當儒瓦可積的函式必是佩龍可積的，且積分值相等；

亞歷山德羅夫(Anexcafippos, II. C.)與羅曼(Looman,H.)於1924年各自獨立地證明了佩龍可積的函式必是狹義當儒瓦可積的，且積分值相等。