基本介紹
- 中文名：瓦爾德積分
- 外文名：Ward integral
- 適用範圍：數理科學
簡介,相關概念,瓦爾德下函式,瓦爾德上函式,提出者背景,
簡介
設f(x)是定義在[a,b]上的函式，H(x)與G(x)分別為f( x)的瓦爾德上函式與下函式。若等式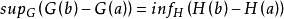
成立，則稱f(x)在[a,b]上依瓦爾德的意義可積，簡稱(W)可積，並將上述上、下確界的公共值稱為f(x)在[a,b]上的瓦爾德積分。
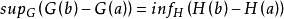
相關概念
瓦爾德下函式
瓦爾德下函式是為定義瓦爾德積分而引進的概念。
設f(x)與G(x)是定義在[a,b]上的函式，若對任意ξ∈[a,b]，存在δ(ξ)>0，使當ξ∈[u,v]⊂(ξ-δ(ξ),ξ+δ(ξ))時有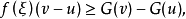
則稱H(x)為f(x)的瓦爾德下函式。
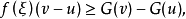
瓦爾德上函式
設f(x)與H(x)是定義在[a,b]上的函式，若對任意ξ∈[a,b]，存在δ(ξ)>0，使當ξ∈[u,v]⊂(ξ-δ(ξ),ξ+δ(ξ))時有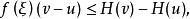
則稱H(x)為f(x)的瓦爾德上函式。
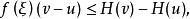
提出者背景
瓦爾德(Wald，Abrahom，1902～1950)美籍羅馬尼亞數理統計學家。生於羅馬尼亞的克羅日，卒於印度。
先就讀於克羅日大學，1927年入維也納大學學習統計學與經濟學，從師門格，1931年獲博士學位。
1938年到美國，在哥倫比亞大學工作，1943年任副教授，1944年任教 授，1946年被任命為新建立的數理統計系的執行官員。
