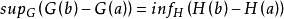瓦爾德下函式是為定義瓦爾德積分而引進的概念,與之對應的是瓦爾德上函式。
基本介紹
- 中文名:瓦爾德下函式
- 外文名:Ward lower function
- 適用範圍:數理科學
定義,瓦爾德上函式,瓦爾德積分,
定義
瓦爾德下函式是為定義瓦爾德積分而引進的概念。
設f(x)與G(x)是定義在[a,b]上的函式,若對任意ξ∈[a,b],存在δ(ξ)>0,使當ξ∈[u,v]⊂(ξ-δ(ξ),ξ+δ(ξ))時有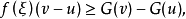 則稱H(x)為f(x)的瓦爾德下函式。
則稱H(x)為f(x)的瓦爾德下函式。
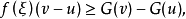
瓦爾德上函式
設f(x)與H(x)是定義在[a,b]上的函式,若對任意ξ∈[a,b],存在δ(ξ)>0,使當ξ∈[u,v]⊂(ξ-δ(ξ),ξ+δ(ξ))時有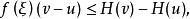 則稱H(x)為f(x)的瓦爾德上函式。
則稱H(x)為f(x)的瓦爾德上函式。
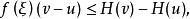
瓦爾德積分
(Ward integral)
設f(x)是定義在[a,b]上的函式,H(x)與G(x)分別為f( x)的瓦爾德上函式與下函式。若等式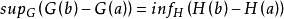 成立,則稱f(x)在[a,b]上依瓦爾德的意義可積,簡稱(W)可積,並將上述上、下確界的公共值稱為f(x)在[a,b]上的瓦爾德積分。
成立,則稱f(x)在[a,b]上依瓦爾德的意義可積,簡稱(W)可積,並將上述上、下確界的公共值稱為f(x)在[a,b]上的瓦爾德積分。