基本介紹
定義定律,定律特點,實驗驗證,適用範圍,發展簡史,套用領域,定律影響,
定義定律
定律特點
牛頓第三運動定律研究的是物體之間相互作用制約聯繫的機制，研究的對象至少是兩個物體，多於兩個以上的物體之間的相互作用，總可以區分成若干兩兩相互作用的物體對。
作用力和反作用力是相互的，互相依賴相為依存，均以對方存在為自已存在的前提，沒有反作用力的作用力是不存在的；力具有物質性，不能脫離開物體（物質）而存在；力總是兩個以上物體之間的相互作用產生的。
牛頓第三定律也具有瞬時性，即作用力和反作用力的同時性，它們是同時產生、同時消失、同時變化，作用力與反作用力的地位是對等的，稱誰為作用力誰為反作用力是無關緊要的。
作用力和反作用力必須是同一性質的力，即作用力為彈力反作用力也一定是彈力，反之亦然。而自然界僅有四類基本的相互作用，即電磁相互作用、引力相互作用、強相互作用和弱相互作用，所以從本質上區分力的性質也僅存在這四種，作用力與反作用力確實必須屬於同一性質的力。
作用力和反作用力不能求和，即不能將第三定律寫成
，原因是作用力和反作用力分別作用在兩個不同的物體上，各自產生的作用效果不同。作用力與反作用力的作用效果不能相互抵消。
實驗驗證
| 實驗驗證方法 | 圖示 |
|---|---|
定性實驗： 取一根長約15厘米兩端開口的細玻璃管，管的值徑約3毫米（能使火柴進出），用兩根火柴裝入管中，使火柴頭在管的中間互相接觸，然後放平。用酒精燈對準火柴頭加熱、不久因玻璃管受熱升溫。火柴頭達到著火點迅速燃燒，氣體相互壓迫，兩根火柴桿從兩管的開口處同時飛出，並觀察到繼續燃燒，飛出的路程大約相等，說明物體的作用是相互的。 |  |
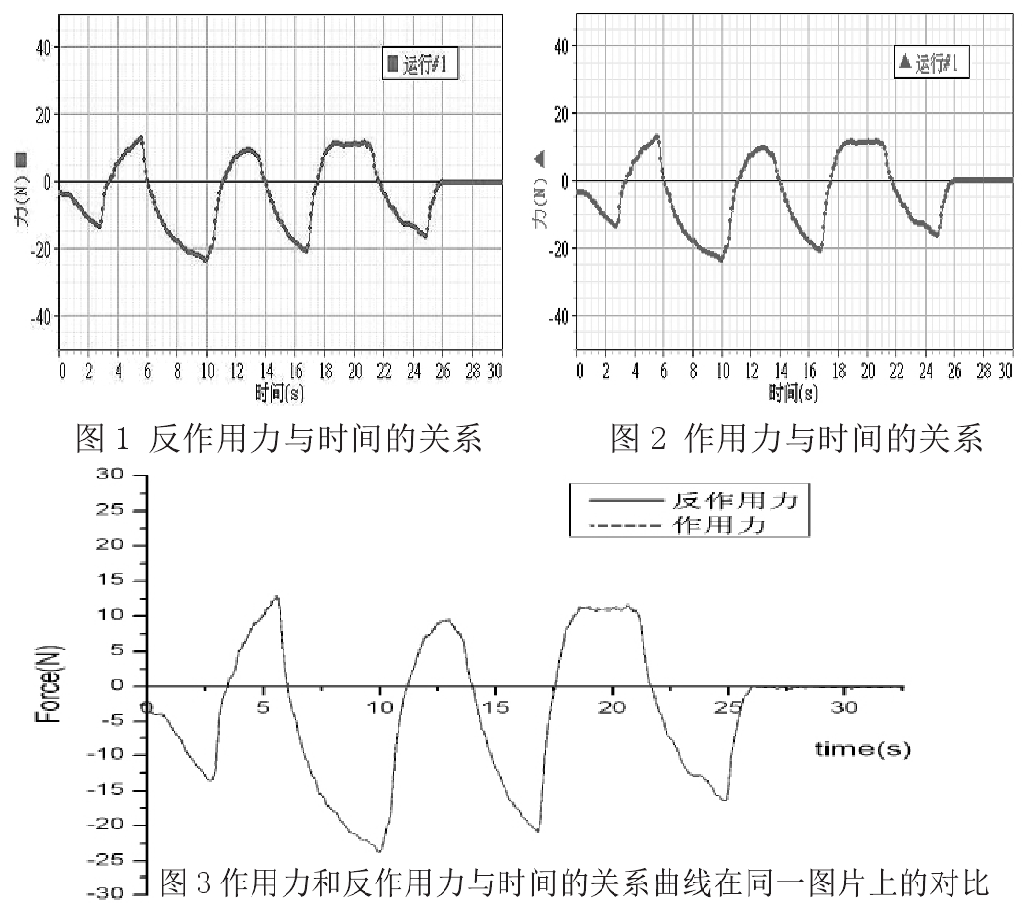
定量實驗： 選取兩個力學感測器，保持兩個感測器在同一平面上，讓兩感測器的測力鉤相互鉤住或相抵，通過數據採集軟體可以分別得到兩條力-時間圖線，如圖1和圖 2所示，同時得到該時間段的作用力和反作用力隨時間變化的實時數據。通過觀察，可以看出作用力和反作用力與時間的對應關係，任意時刻這兩個個力的大小基本一致，表示兩個力大小相等。 這種實驗方案，不僅適用於量化水平面上的相互作用力，而且適用於量化豎直平面或與豎直方向成任意角度的同一平面上的相互作用力，只要和兩個力處於同一平面，就可以精確模擬作用力與反作用力，體現了兩個物體之間的作用力和反作用力總是大小相等，作用在同一直線上，更加直觀有效的突出牛頓第三定律的普適性。 |  |
適用範圍
牛頓第三運動定律只適用於慣性系中實物物體之間的相互作用，如在電磁場中運動的電子，將受到電磁場力作用，但無從談論電子對電磁場的反作用力；非慣性系中的慣性力無反作用力；由場參與的相互作用，其作用傳遞是需要時間，作用與反作用的同時性不成立。第三定律是獨立的，但也存在適用範圍。
第三定律在類似“無論相互作用的兩物體是靜止的還是運動的，該定律都成立”的表述後，曾被加上一段說明，“如果把該定律套用於電磁場將會遇到困難……分別作用於帶電粒子的力，並不符合該定律”或“不能把該定律推廣到相對論中”或“不能把該定律推廣到運動帶電粒子上”或“電磁場是一個特別麻煩的系統，當這樣的場出現時，就會引起佯謬……該定律明顯失效……如果把場考慮進去，佯謬就可以在牛頓體系中得到解決”或“該定律不是經常正確的，但它在接觸相互作用（即在物體直接接觸情況下，觀察到的相互作用）以及彼此間‘有一定距離的靜止物體相互作用的情況下是完全嚴格成立的”等。如將該律表述為：“兩接觸物體（包括粒子和場）之間的作用和反作用，大小相等，方向相反，作用在一條直線上”，那么一切“失效”、“不成立”之說都不復存在。雖然新舊錶述只是“接觸”兩字之差，但卻更明顯地反映了近距作用的觀點，這樣的表述既適用於電磁相互作用，又可推廣到相對論中。
在經典力學中，第三定律成立的條件是：巨觀物體作低速運動。當物體的運動速度接近光速時，作用力和反作用的大小一般不再相等。對於接觸力，該定律嚴格成立，對於非接觸力，例如萬有引力和電磁力，由於相互作用通過場以有限速度傳播，需要考慮推遲效應。具體到引力作用，由於在普遍力學問題中，物體相距較近，而相對運動速度又不大，且認為引力場是穩恆的，故該定律仍成立（嚴格說應是“近似成立”）。至於電磁力的情形，對於電磁作用除了需考慮推遲效應外，還需考慮另一個因素。由於兩個帶電體系之間的相互作用是靠第三者——電磁場來傳遞，故參與電磁相互作用的客體不再只是兩個，而是三個，因而情形就變得複雜些。若將三個客體（即兩個帶電體系和電磁場）視為一個封閉系統，由電動力學可知，當客體的運動狀態發生改變時，整個系統的動量依然守恆。在電磁現象中，對於兩帶電體系在穩恆場中的相互作用，第三定律成立（嚴格說是近似成立），對於發生在變化場中的相互作用，該定律不再成立。由於電磁現象中的多數情形為非穩恆場，故該定律在電磁現象中一般不成立。一般說來，微觀粒子不再遵從該定律，但在經典的分子熱運動中，對於分子之間的碰撞問題，仍可使用該定律。
發展簡史
十七世紀中葉，碰撞問題成為科學界共同關心的課題，不少科學家都致力於該問題的研究。當時，對碰撞問題研究較早的有笛卡爾。1664年，牛頓受到笛卡爾的影響，也開始研究二個球形非彈性剛體的碰撞問題。1665—1666年間牛頓又研究了二個球形剛體的碰撞問題。他沒有像其它科學家那樣把注意力集中在動量和動量守恆方面，而是把注意力放在物體之間的相互作用上，對於兩剛體的碰撞，他提出，“……一於是在它們向彼此運動的時間中（就是它們相碰的瞬間）它們的壓力處於最大值，……它們的整個運動是被此一瞬間彼此之間的壓力所阻止，……只要這兩個物體都不互相屈服，它們之間將會持有同樣猛烈的壓力，……它們將會象以前彈回之前彼此趨近那樣多的運動相互離開。”
上面這段話可看出，牛頓當時就已認識到在物體相互碰撞的瞬間，它們的運動被彼此之間的壓力所改變。稍後，牛頓又認識到：“如果二物體p和r彼此相遇，因為p壓r和r壓p是一樣大小，所以二者的阻力是相同的。”同時他還用圖形明確表示p壓r和r壓p的力是在同一條直線上。
由此可見，牛頓在1665—1666年間就已經意識到了牛頓第三定律的全部內容，但是將它作用牛頓運動三定律之一在《自然哲學的數學原理》一書中正式提出，卻是20多年以後的事，在1668—1669年間，惠更斯、沃里斯和雷恩對碰撞問題也做了很多研究工作，並得出了一些重要的結論，其中惠更斯的工作比較突出。他證明了兩硬體在碰撞過程中同一方向的動量保持不變，糾正了笛卡爾不考慮動量具有方向性的錯誤，而且首次提出碰撞前後的動量守恆。牛頓在正式提出第三定律時肯定了他們的工作，同時也指出了他們的局限性。牛頓認為:“雷恩和惠更斯的理論以絕對硬的物體為前提，而用理想彈性體可以得到更肯定的結果，並且用非理想彈性體，如壓緊的木球、鋼球和玻璃球做實驗，消除誤差後結果是一致的。”
1666年初，牛頓創立了三大運動定律，這些定律為他發明微積分和發現地球引力創造了必不可少的條件。但直到20年後哈雷鼓勵牛頓寫《自然哲學的數學原理》時，牛頓才公布了他創立的三大定律。
1673年，馬利奧用兩個單擺做碰撞實驗，巧妙地測出了碰撞前後的瞬時速度。牛頓也重複做了此實驗，他進一步討論了空氣阻力的影響及改進辦法，並對結果進行了修正。
這樣，牛頓正是從研究、總結碰撞問題出發提出了作用與反作用定律，並從理論和實驗兩方面進行了驗證。1687年，牛頓才正式將第三定律作為“運動定律三”提了出來，他寫道：:“每一個作用總有一個大小相等而方向相反的反作用;或者說，兩個物體的相互作用總是大小相等方向相反。”1684年，讓·皮卡爾第一次精確地求出了地球的大小和質量。有了這些必要的數字，牛頓就能證明：利用三大運動定律和他的重力方程式可以正確地計算出行星運動的真實軌道。即使有了確鑿的數學證據，牛頓也只是在哈雷的請求和說服下於1687年發表了《自然哲學的數學原理》，發表這本書最主要的原因是羅伯特·胡克錯誤地聲稱他自己已經發現了運動的普遍規律。
從牛頓第三定律的發現過程可以看出，牛頓從力的觀點出發研究碰撞問題時發現作用與反作用定律，他是在別人對動量研究的基礎上，更深入一步，從而揭示了兩物體碰撞時力的相互作用規律的。因此，如果說牛頓第一、第二定律是牛頓在總結前人工作的基礎上提出的話，那么牛頓第三定律則完全是牛頓本人獨立作出的偉大發現。
套用領域
牛頓第三運動定律是研究質點系運動規律的基礎，一般來說接觸物體之間相互作用都遵從該定律，對於相隔一定距離物體之間的相互作用要看具體情況。
在A物體給B物體一個作用力F的同時，B物體也給A物體一個反作用力F反。當B物體靜止時F反=-F，當B物體運動（或者作用點滑動）時F反<-F，這時反作用力等於B物體在F的作用下運動所受到的阻力F阻，即F反=F阻。綜合上述兩種狀況得：F反=F阻≤-F。以根據“空吸（卷吸）作用”原理設計一種尾噴管，從輪船的後側面吸水經尾噴管噴出，通過增加噴水量來獲得更大的反作用力，從而提高推進效率。此外，F反=F阻≤-F還能廣泛用於指導飛機、火箭和車輛等運動機械的製造設計，對於提高它們的推進效率都會大有幫助。
定律影響
牛頓第三運動定律不僅揭示兩物體相互作用的規律，而且為解決力學問題，轉換研究對象提供了理論基礎，拓寬了牛頓第二定律的適用範圍，是牛頓物理學中不可分割的重要組成部分。
於是由僅關注單一物體（只研究一個物體）的第一定律和第二定律出發，結合第三定律擴展了研究對象，就自然而然地解決了全部不論多么複雜的系統的動力學問題了。第三定律是確實是完全獨立的基本規律，它不能由第二定律推演得出，第二定律也代替不了第三定律，第一定律更不能取代第三定律。
