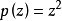伯恩施坦一魯賓孫定理

伯恩施坦一魯賓孫定理，英文名為Bernstein-Robinson theorem，是關於不變子空間的一個定理，由Abraham Robinson和Allen R. Bernstein提出，秉屬於泛函分析下的希爾伯特空間分支。

基本介紹

• 中文名：伯恩施坦一魯賓孫定理
• 外文名：Bernstein-Robinson theorem
• 提出者：A.博恩斯坦，A.R.羅賓森
• 提出時間：1966
• 套用學科：數學
• 適用領域範圍：泛函分析
• ：

簡介

關於不變子空間的一個定理.該定理斷言:

設T為複數域上無限大希爾伯特空間H上的有界線性運算元，p(z)≠0為復係數多項式，使p(T)完全連續(緊緻)，且 ,那么T使得H的至少一個非H非{0}的閉線性子空間不變。

發展歷史

20世紀30年代，馮·諾伊曼(vonNeumann , J.)證明了希爾伯特空間上的緊運算元具有非平凡的不變子空間.

於是非緊運算元是否具有不變子空間的問題便由K. T. Smith和P.R.Halmos於1963年提出，但是一直沒有大的進展.

1966年，伯恩施坦(Bernstein, A. R.)（1918.10.6-1972.4.11)，及魯賓孫(Robinson, A.)首先用非標準分析在證明了上述結果，發表在《Pacfic Journal of Mathematic》s期刊上。